题目内容
10.如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,下列结论中能成立的序号为④.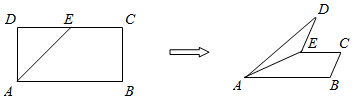
①ED⊥平面ACD
②CD⊥平面BED
③BD⊥平面ACD
④AD⊥平面BED.
分析 在折起过程中,画出D点在平面BCE上的投影轨迹,利用线面垂直的判定定理即可逐项判断得解.
解答  解:∵在矩形ABCD中,AB=8,BC=4,E为DC边的中点
解:∵在矩形ABCD中,AB=8,BC=4,E为DC边的中点
∴在折起过程中,D点在平面BCE上的投影如右图.
∵DE与AC所成角不能为直角,
∴DE不会垂直于平面ACD,故①错误;
只有D点投影位于O2位置时,即平面AED与平面AEB重合时,
才有BE⊥CD,此时CD不垂直于平面AEBC,
故CD与平面BED不垂直,故②错误;
BD与AC所成角不能成直线,
∴BD不能垂直于平面ACD,故③错误;
∵AD⊥ED,并且在折起过程中,有AD⊥BC,
∴存在一个位置使AD⊥BE,
∴在折起过程中AD⊥平面BED,故④正确.
故答案为:④.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意线面垂直的判定定理的合理运用.

练习册系列答案
相关题目
18.已知点M是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,F是其右焦点,P为线段MF的中点,若|OM|=|OF|(0为坐标原点)且|OP|=$\frac{1}{2}$a,则双曲线的离心率为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
2.点G为△ABC的重心,设$\overrightarrow{BG}$=$\overrightarrow{a}$,$\overrightarrow{GC}$=$\overrightarrow{b}$,则$\overrightarrow{AB}$=( )
| A. | $\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$ | B. | $\frac{3}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C. | $\overrightarrow{b}$-2$\overrightarrow{a}$ | D. | 2$\overrightarrow{a}+\overrightarrow{b}$ |
19.已知数列{an}的前n项和为Sn,满足nSn+1-(n+1)Sn=2n2+2n(n∈N*),a1=3,则数列{an}的通项an=( )
| A. | 4n-1 | B. | 2n+1 | C. | 3n | D. | n+2 |
20.已知tanα=2,α为第一象限角,则sin2α+cosα的值为( )
| A. | $\sqrt{5}$ | B. | $\frac{{4+2\sqrt{5}}}{5}$ | C. | $\frac{{4+\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}-2}}{5}$ |
