��Ŀ����
15�����ں���y=f��x������x0����f��x0��=x0�����x0λ����f��x����һ�ײ����㣬��x0����f��f��x0����=x0�����x0λ����f��x���Ķ��ײ����㣬��x0����f��f��x0����=x0����f��x0����x0�����x0Ϊ����f��x���Ķ������ڵ㣮��1����f��x��=kx+1��
�ٵ�k=2ʱ������f��x���Ķ��ײ����㣬���ж����Ƿ��Ǻ���f��x���Ķ������ڵ㣻
����֪����f��x�����ڶ������ڵ㣬��k��ֵ��
��2����������ʵ��b������g��x��=x2+bx+c�����ڶ������ڵ㣬��ʵ��c��ȡֵ��Χ��
���� ��1���ٵ�k=2ʱ��f��x��=2x+1����϶��ײ�����Ͷ������ڵ�Ķ��壬�ɵô𰸣�
���ɶ������ڵ�Ķ��壬���f��x��=kx+1�����������������kֵ��
��2����������ʵ��b������g��x��=x2+bx+c�����ڶ������ڵ㣬����g��x��=x2+bx+c=x�����������ȵ�ʵ��������ô𰸣�
��� �⣺��1���ٵ�k=2ʱ��f��x��=2x+1��
f��f��x����=2��2x+1��+1=4x+3��
��4x+3=x�ã�x=-1��
��-1Ϊ����f��x���Ķ��ײ����㣬
ʱf��-1��=-1��
��-1���Ǻ���f��x���Ķ������ڵ㣻
�ڡ�f��x��=kx+1��
��f��f��x����=k2x+k+1��
��f��f��x����=x��
��x=$\frac{k+1}{1-{k}^{2}}$=$\frac{1}{1-k}$����k�١�1������x=0��k=-1��
��f��x��=x����x=$\frac{1}{1-k}$��
������f��x�����ڶ������ڵ㣬��k=-1��
��2����x0Ϊ����f��x���Ķ������ڵ㣮
��f��f��x0����=x0����f��x0����x0��
��x1Ϊ����f��x���Ķ��ײ����㣬
��f��f��x1����=x1����f��x1��=x1��
��f��x0��=f��x1����
��x0��x1����f��x0��+f��x1��=-b��
������g��x��=x2+bx+c=x�����������ȵ�ʵ������
�ʡ�=��b-1��2-4c��0�������
��ã�c��0��
���� �����Զ��ײ�����Ͷ������ڵ�Ϊ���壬�����˶��κ����Ļ������ʣ���ȷ������ײ�����Ͷ������ڵ�ĸ����ǽ��Ĺؼ���

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�| A�� | ?x0��R��f��x0��=0 | |
| B�� | ��x0��f��x���ļ�Сֵ�㣬��f��x�������䣨-�ޣ�x0���ϵ����ݼ� | |
| C�� | ����f��x����ͼ�������ĶԳ�ͼ�� | |
| D�� | ��x0��f��x���ļ�ֵ�㣬��f�䣨x0��=0 |
| A�� | ?x�ʣ�0��$\frac{��}{2}$����ʹ��cosx��x | B�� | ?x�ʣ�0��$\frac{��}{2}$����ʹ��cosx��x | ||
| C�� | ?x�ʣ�0��$\frac{��}{2}$����ʹ��cosx��x | D�� | ?x�ʣ�0��$\frac{��}{2}$����ʹ��cosx��x |
| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{3}}}{2}$ | C�� | $-\frac{1}{2}$ | D�� | $-\frac{{\sqrt{3}}}{2}$ |
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |
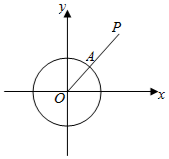 ��ƽ��ֱ������ϵxOy�У����ڡ�O��x2+y2=1��˵��P������ϵ������һ�㣬��P����O�ľ���SP�Ķ������£���P��O�غϣ�SP=r����P����O�غϣ�����OP���O�Ľ���ΪA��SP=AP�ij��ȣ���ͼ����
��ƽ��ֱ������ϵxOy�У����ڡ�O��x2+y2=1��˵��P������ϵ������һ�㣬��P����O�ľ���SP�Ķ������£���P��O�غϣ�SP=r����P����O�غϣ�����OP���O�Ľ���ΪA��SP=AP�ij��ȣ���ͼ����