题目内容
20．
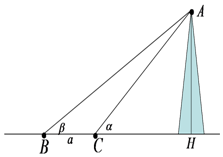如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）| A． | $\frac{asinαsinβ}{{sin（{α-β}）}}$ | B． | $\frac{asinαcosβ}{{sin（{α-β}）}}$ | C． | $\frac{acosαsinβ}{{sin（{α-β}）}}$ | D． | $\frac{acosαcosβ}{{sin（{α-β}）}}$ |
分析 利用正弦定理，及直角三角形中的三角函数，即可得出结论．
解答 解：△ABC中，$\frac{a}{sin（α-β）}=\frac{AB}{sin（π-α）}$，∴AB=$\frac{asinα}{sin（α-β）}$，
△ABH中，AH=$\frac{asinαsinβ}{{sin（{α-β}）}}$，
故选A．
点评 本题考查正弦定理，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
15．在△ABC中，a、b、c分别是角A、B、C的对边，若A=$\frac{π}{3}$，c=1，△ABC的面积为$\sqrt{3}$，则a的值为（ ）
| A． | 2 | B． | 4 | C． | $2\sqrt{3}$ | D． | $\sqrt{13}$ |
某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．