题目内容
10．
某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图，每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）．（1）求居民收入在[3000，3500）的频率；
（2）根据频率分布直方图算出样本数据的中位数、平均数
及其众数；
（3）为了分析居民的收入与年龄、职业等方面的关系，按收入从这10000人中用分层抽样方法抽出100人作进一步分析，则应在月收入为[2500，3000）的人中抽取多少人？
分析 （1）根据频率=小矩形的高×组距来求；
（2）根据中位数的左右两边的矩形的面积和相等，所以只需求出从左开始面积和等于0.5的底边横坐标的值即可，运用取中间数乘频率，再求之和，计算可得平均数；
（3）求出月收入在[2500，3000）的人数，用分层抽样的抽取比例乘以人数，可得答案．
解答 解：（1）居民收入在[3000，3500）的频率为0.0003×500=15%．
（2）中位数为$2000+500×\frac{4}{5}=2400$，
平均数为1250×10%+1750×20%+2250×25%+2750×25%+3250×15%+3750×5%=2400，其众数2250，2750．
（3）在月收入为[2500，3000）的人中抽取25人．
点评 本题考查了频率分布直方图，分层抽样方法，是统计常规题型，解答此类题的关键是利用频率分布直方图求频数或频率．
练习册系列答案
相关题目
20．
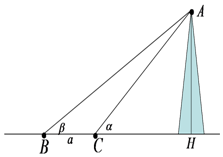如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）
如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）| A． | $\frac{asinαsinβ}{{sin（{α-β}）}}$ | B． | $\frac{asinαcosβ}{{sin（{α-β}）}}$ | C． | $\frac{acosαsinβ}{{sin（{α-β}）}}$ | D． | $\frac{acosαcosβ}{{sin（{α-β}）}}$ |
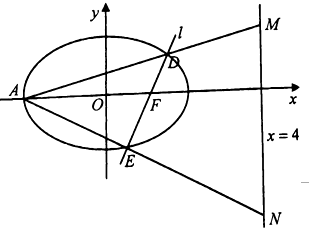已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，短轴长为2$\sqrt{3}$，点P为椭圆C上一点，且点P到点F的最远距离是最近距离的3倍．