题目内容
10．已知p：x≥a，q：|x-1|＜1，若p是q的必要不充分条件，则实数a的取值范围是a≤0．分析 根据不等式的性质，结合充分条件和必要条件的定义，建立不等式关系进行求解即可．
解答 解：由|x-1|＜1得-1＜x-1＜1得0＜x＜2，
若p是q的必要不充分条件，
则a≤0，
故答案为：a≤0
点评 本题主要考查充分条件和必要条件的应用，根据定义建立不等式关系是解决本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
1．函数$f（x）=\frac{1}{{\sqrt{{x^2}-1}}}+lg（{2+x}）$的定义域是（ ）
| A． | （-2，-1） | B． | （-2，1） | C． | （-2，-1）∪（1，+∞） | D． | （-2，+∞） |
5．若三角形的三条边之比为3：5：7，与它相似的三角形的最长边为21cm，则其余两边的长度之和为（ ）
| A． | 24cm | B． | 21cm | C． | 19cm | D． | 9cm |
15．若点P到点F（2，0）的距离比它到直线x+3=0的距离小1，则点P的轨迹方程是（ ）
| A． | y2=2x | B． | y2=4x | C． | y2=8x | D． | x2=8y |
19．从直线x-y+3=0上的点向圆x2+y2-4x-4y+7=0引切线，则切线长的最小值为（ ）
| A． | $\frac{3\sqrt{2}}{2}$ | B． | $\frac{\sqrt{14}}{2}$ | C． | $\frac{3\sqrt{2}}{4}$ | D． | $\frac{3\sqrt{2}}{2}$-1 |
20．
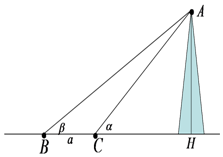如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）
如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）| A． | $\frac{asinαsinβ}{{sin（{α-β}）}}$ | B． | $\frac{asinαcosβ}{{sin（{α-β}）}}$ | C． | $\frac{acosαsinβ}{{sin（{α-β}）}}$ | D． | $\frac{acosαcosβ}{{sin（{α-β}）}}$ |