题目内容
11．已知过点A（-2，m）和点B（m，4）的直线为l1，l2：2x+y-1=0，l3：x+ny+1=0．若l1∥l2，l2⊥l3，则实数m+n的值为（ ）| A． | -10 | B． | -2 | C． | 0 | D． | 8 |
分析 利用直线平行垂直与斜率的关系即可得出．
解答 解：∵l1∥l2，∴${k_{AB}}=\frac{4-m}{m+2}=-2$，解得m=-8．
又∵l2⊥l3，∴$（{-\frac{1}{n}}）×（{-2}）=-1$，解得n=-2．
∴m+n=-10．
故选：A．
点评 本题考查了直线平行垂直与斜率的关系，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
1．函数$f（x）=\frac{1}{{\sqrt{{x^2}-1}}}+lg（{2+x}）$的定义域是（ ）
| A． | （-2，-1） | B． | （-2，1） | C． | （-2，-1）∪（1，+∞） | D． | （-2，+∞） |
19．从直线x-y+3=0上的点向圆x2+y2-4x-4y+7=0引切线，则切线长的最小值为（ ）
| A． | $\frac{3\sqrt{2}}{2}$ | B． | $\frac{\sqrt{14}}{2}$ | C． | $\frac{3\sqrt{2}}{4}$ | D． | $\frac{3\sqrt{2}}{2}$-1 |
传说古希腊毕达哥拉斯（Pythagoras，约公元前570年&公元前500年）学派的数学家经常在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数．根据下列四个图形及相应的正方形的个数的变化规律，第n个图形中有$\frac{n（n+1）}{2}$个正方形．
20．
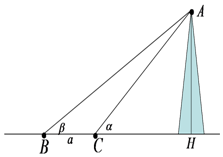如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）
如图，在点B处测得山顶A的仰角为β，在点C处测得山顶A的仰角为α，BC=a，则山高AH为（ ）| A． | $\frac{asinαsinβ}{{sin（{α-β}）}}$ | B． | $\frac{asinαcosβ}{{sin（{α-β}）}}$ | C． | $\frac{acosαsinβ}{{sin（{α-β}）}}$ | D． | $\frac{acosαcosβ}{{sin（{α-β}）}}$ |