题目内容

已知正项等比数列{an}中，a2•a5•a13•a16=256，a7=2则数列{an}的公比为（　　）
A、
2
B、2
C、±2
D、±
2
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由题意和等比数列的性质可得a94=256，解得a9由通项公式可得公比．
解答： 解：∵正项等比数列{an}中，a2•a5•a13•a16=256，
∴a94=a2•a5•a13•a16=256，解得a9=4，
又a7=2，∴数列{an}的公比q=
a9
a7
=
2

故选：A．
点评：本题考查等比数列的通项公式，涉及等比数列的性质，属基础题．
练习册系列答案
相关题目
已知函数f（x）=sin（2x+
π
4
）（x∈R）的最小正周期为π，为了得到函数g（x）=sin2x的图象，只要将y=f（x）的图象（　　）
A、向左平移
π
8
个单位长度
B、向右平移
π
8
个单位长度
C、向左平移
π
4
个单位长度
D、向右平移
π
4
个单位长度
已知函数f（x）=x2+2x|x+a|，其中a∈R．求函数f（x）的单调区间．
下列命题中，正确命题的个数为（　　）
①“若xy=0，则x=0或y=0”的逆否命题为“若x≠0且y≠0，则xy≠0”；
②若随机变量X服从正态分布N（3，σ2），且P（X≤6）=0.72，则P（X≤0）=0.28；
③函数f（x）的导函数满足f′（x0）=0，则函数f（x）在x=x0处有极值．
A、0B、1C、2D、3
双曲线x2-2y2=4的虚轴长是（　　）
A、2
B、
2
C、4
D、2
2
若f（x）=
1
x2-x+3
，则f′（x）等于
 
．
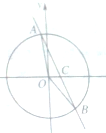如图所示，在平面坐标系中，直线y=-2x+b（0＜b＜1）与单位圆x2+y2=1相交于A，B（A在第二象限）两个不同的点，且∠AOB=α，∠BOC=β，则cos（α-2β）的值是（　　）
A、-
3
5
B、
3
5
C、-
4
3
D、
4
3
已知等差数列{an}，且a4+a8=2，则a6（a2+2a6+a10）的值为（　　）
A、4B、6C、8D、10
已知函数f(x)=lg(1-
a
2x
)的定义域是(
1
2
，+∞)，则实数a的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网