题目内容
已知a∈R,命题p:实系数一元二次方程x2+ax+2=0的两根都是虚数;命题q:存在复数z同时满足|z|=2且|z+a|=1.
(1)若命题p中根的虚部为整数,求实数a的值;
(2)若命题p、q同为真命题,求实数a的取值范围.
(1)若命题p中根的虚部为整数,求实数a的值;
(2)若命题p、q同为真命题,求实数a的取值范围.
考点:二次函数的性质,复数代数形式的混合运算
专题:计算题,函数的性质及应用,数系的扩充和复数
分析:(1)由实系数一元二次方程x2+ax+2=0的两根都是虚数知△=a2-8<0,再令
为非零整数求a;
(2)求命题p、q为真,再判断都为真时的要求即可.
±
| ||
| 2 |
(2)求命题p、q为真,再判断都为真时的要求即可.
解答:
解:(1)由已知可得△=a2-8<0,
∴-2
<a<2
,
于是方程的根为
,
由方程的虚部为整数时,
为非零整数,
∴a=±2.
(2)若命题p为真命题,由(1)得,-2
<a<2
,
若命题q为真命题,
则复平面上的圆x2+y2=4和圆(x+a)2+y2=1有交点,
于是1≤|a|≤3,
故两个命题同时为真,则实数a的取值范围是(-2
,-1]∪[1,2
).
∴-2
| 2 |
| 2 |
于是方程的根为
-a±
| ||
| 2 |
由方程的虚部为整数时,
±
| ||
| 2 |
∴a=±2.
(2)若命题p为真命题,由(1)得,-2
| 2 |
| 2 |
若命题q为真命题,
则复平面上的圆x2+y2=4和圆(x+a)2+y2=1有交点,
于是1≤|a|≤3,
故两个命题同时为真,则实数a的取值范围是(-2
| 2 |
| 2 |
点评:本题考查了二次方程的根的存在性及复数的定义,同时考查了复数的几何意义及命题的真假性的判断,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x是菱形},B={x|x是正方形},C={心x|x是平行四边形},那么A,B,C之间的关系是( )
| A、A⊆B⊆C |
| B、B⊆A⊆C |
| C、A?B⊆C |
| D、A=B⊆C |
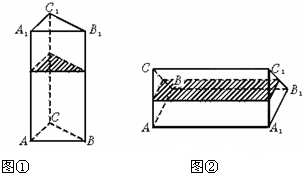 如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?
如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?