题目内容
2．
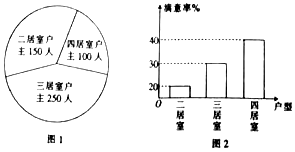已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用分层抽样的方法抽取20%的户主进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（ ）| A． | 100，8 | B． | 80，20 | C． | 100，20 | D． | 80，8 |
分析 利用统计图结合分层抽样性质能求出样本容量，利用条形图能求出抽取的户主对四居室满意的人数．
解答 解：样本容量为：（150+250+100）×20%=100，
∴抽取的户主对四居室满意的人数为：100×$\frac{100}{150+250+100}×40%=8$．
故选：A．
点评 本题考查样本容量和抽取的户主对四居室满意的人数的求法，是基础题，解题时要认真审题，注意统计图的性质的合理运用．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12．已知i是虚数单位，复数z满足（i-1）z=i，则z的虚部是（ ）
| A． | $\frac{1}{2}$ | B． | $-\frac{1}{2}i$ | C． | $\frac{1}{2}i$ | D． | $-\frac{1}{2}$ |
13．已知函数f（x）=ex-ax+b（a，b∈R）．
（1）若f（x）在x=0处的极小值为2，求a，b的值；
（2）设g（x）=f（x）+ln（x+1），当x≥0时，g（x）≥1+b，试求a的取值范围．
（1）若f（x）在x=0处的极小值为2，求a，b的值；
（2）设g（x）=f（x）+ln（x+1），当x≥0时，g（x）≥1+b，试求a的取值范围．
10．为了解人们对于国家新颁布的“生育二孩放开”政策的热度，现在对某市年龄在35岁的人调查，随机选取年龄在35岁的100人进行调查，得到他们的情况为：在55名男性中，支持生二孩的有40人，不支持生二孩的有15人；在45名女性中，支持生二孩的有20人，不支持的有25人．
（Ⅰ）完成下面2×2列联表，并判断有多大的把握认为“支持生二孩与性别有关”？
附：K2=$\frac{{n（ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
（Ⅱ）在被调查的人员中，按分层抽样的方法从支持生二孩的人中抽取6人，再用简单随机抽样的方法从这6人中随机抽取2人，求这2人中恰好有1名男性的概率；
（Ⅲ）以上述样本数据估计总体，从年龄在35岁人中随机抽取3人，记这3人中支持生二孩且为男性的人数为X，求X的分布列和数学期望．
（Ⅰ）完成下面2×2列联表，并判断有多大的把握认为“支持生二孩与性别有关”？
| 支持生二孩 | 不支持生二孩 | 合计 | |
| 男性 | 40 | 15 | 55 |
| 女性 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
| P（K2≥k0） | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（Ⅲ）以上述样本数据估计总体，从年龄在35岁人中随机抽取3人，记这3人中支持生二孩且为男性的人数为X，求X的分布列和数学期望．
14．对数列{an}，“an＞0对于任意n∈N*成立”是“其前n项和数列{Sn}为递增数列”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充分必要条件 | D． | 非充分非必须条件 |