题目内容
7.在△ABC中,角A、B、C的对边分别为a,b,c,且$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$=$\frac{cosC}{cosA}$.(Ⅰ)求角A的值;
(Ⅱ)若B=$\frac{π}{6}$,且△ABC的面积为4$\sqrt{3}$,求BC边上的中线AM的大小.
分析 (I)$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$=$\frac{cosC}{cosA}$,利用正弦定理化为2sinBcosA-$\sqrt{3}$sinCcosA=$\sqrt{3}$sinAcosC,再利用和差公式即可得出.
(II)A=B=$\frac{π}{6}$,可得C=$\frac{2π}{3}$.a=b,$\frac{1}{2}{a}^{2}$sin$\frac{2π}{3}$=4$\sqrt{3}$,解得a.c=2bcos$\frac{π}{6}$.在△ABM中,由余弦定理即可得出.
解答 解:(I)∵$\frac{2b-\sqrt{3}c}{\sqrt{3}a}$=$\frac{cosC}{cosA}$,∴2sinBcosA-$\sqrt{3}$sinCcosA=$\sqrt{3}$sinAcosC,
化为:2sinBcosA=$\sqrt{3}$sin(C+A)=$\sqrt{3}$sinB,sinB≠0.
∴cosA=$\frac{\sqrt{3}}{2}$,A∈(0,π).
∴A=$\frac{π}{6}$.
(II)A=B=$\frac{π}{6}$,∴C=$\frac{2π}{3}$.
∴a=b,$\frac{1}{2}{a}^{2}$sin$\frac{2π}{3}$=4$\sqrt{3}$,解得a=4=b.
∴c=2bcos$\frac{π}{6}$=4$\sqrt{3}$.
在△ABM中,由余弦定理可得:AM2=$(4\sqrt{3})^{2}+{2}^{2}$-2×$4\sqrt{3}×2$cos$\frac{π}{6}$=28.
∴AM=2$\sqrt{7}$.
点评 本题考查了正弦定理余弦定理、三角形面积计算公式、和差公式,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 2.8kg | B. | 8.9kg | C. | 10kg | D. | 28kg |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
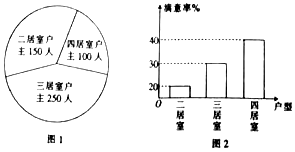 已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )| A. | 100,8 | B. | 80,20 | C. | 100,20 | D. | 80,8 |
| A. | ($\frac{π}{6}$,-1) | B. | ($\frac{π}{3}$,-1) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{3}$,0) |