题目内容
11．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}-1，x≤0}\\{\sqrt{x}，x＞0}\end{array}\right.$若f[f（x0）]=1，则x0=-1或1．分析 当x0≤0时，$f（{x}_{0}）={2}^{-{x}_{0}}-1$，由f（x0）=${2}^{-{x}_{0}}-1＜0$，得f[f（x0）]=f（${2}^{-{x}_{0}}$-1）=${2}^{-{2}^{-{x}_{0}}-1}-1=1$，无解，由$f（{x}_{0}）={2}^{-{x}_{0}}-1$＞0，解得x0=-1；当x0＞0时，f（x0）=$\sqrt{{x}_{0}}$＞0，由f（f（x0））=f（$\sqrt{{x}_{0}}$）=$\sqrt{\sqrt{{x}_{0}}}$=1，解得x0=1．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}-1，x≤0}\\{\sqrt{x}，x＞0}\end{array}\right.$，f[f（x0）]=1，
∴当x0≤0时，$f（{x}_{0}）={2}^{-{x}_{0}}-1$，
当f（x0）=${2}^{-{x}_{0}}-1＜0$时，f[f（x0）]=f（${2}^{-{x}_{0}}$-1）=${2}^{-{2}^{-{x}_{0}}-1}-1=1$，无解，
当$f（{x}_{0}）={2}^{-{x}_{0}}-1$＞0时，$\sqrt{{2}^{-{x}_{0}}-1}$=1，解得x0=-1，成立；
当x0＞0时，f（x0）=$\sqrt{{x}_{0}}$＞0，∴f（f（x0））=f（$\sqrt{{x}_{0}}$）=$\sqrt{\sqrt{{x}_{0}}}$=1，解得x0=1，成立．
综上，x0的值为-1或1．
故答案为：-1或1．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
底面为菱形的直棱柱ABCD-A1B1C1D1中，E、F分别为棱A1B1、A1D1的中点，
2．
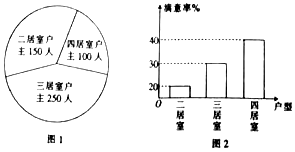已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用分层抽样的方法抽取20%的户主进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（ ）
已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用分层抽样的方法抽取20%的户主进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（ ）| A． | 100，8 | B． | 80，20 | C． | 100，20 | D． | 80，8 |
19．若将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向左平移$\frac{π}{4}$个单位长度，再向下平移1个单位长度，得到函数g（x）的图象，则g（x）的一个对称中心为（ ）
| A． | （$\frac{π}{6}$，-1） | B． | （$\frac{π}{3}$，-1） | C． | （$\frac{π}{6}$，0） | D． | （$\frac{π}{3}$，0） |
6．已知集合A={x|2x-x2≥0}，B={y|y=2x，x∈A}，则A∩B=（ ）
| A． | [0，1） | B． | [1，2] | C． | （2，4] | D． | [2，4] |
2．设函数g（x）是R上的偶函数，当x＜0时，g（x）=ln（1-x），函数$f（x）=\left\{\begin{array}{l}{x^3}，x≤0\\ g（x），x＞0\end{array}\right.$满足f（2-x2）＞f（x），则实数x的取值范围是（ ）
| A． | （-∞，1）∪（2，+∞） | B． | （-∞，-2）∪（1，+∞） | C． | （1，2） | D． | （-2，1） |