题目内容
已知抛物线的焦点F在x轴上,且经过点Q(2,m),点Q到点F的距离为4.
(1)求抛物线的标准方程;
(2)若过M(0,3)作直线交抛物线于A、B,求AB的中点N的轨迹方程.
(1)求抛物线的标准方程;
(2)若过M(0,3)作直线交抛物线于A、B,求AB的中点N的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设抛物线的标准方程为y2=2px,p>0,由已知得2+p=4,由此能求出抛物线的标准方程.
(2)设A(x1,y1),B(x2,y2),中点N(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)分别代入y2=4x,利用点差法有求出AB的中点N的轨迹方程.
(2)设A(x1,y1),B(x2,y2),中点N(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)分别代入y2=4x,利用点差法有求出AB的中点N的轨迹方程.
解答:
解:(1)∵抛物线的焦点F在x轴上,且经过点Q(2,m),
∴设抛物线的标准方程为y2=2px,p>0,
∵点Q到点F的距离为4,
∴2+p=4,解得p=2,
∴抛物线的标准方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),中点N(x,y),
则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入y2=4x,得:
,整理,得(y1+y2)(y1-y2)=4(x1-x2),
即2y(y1-y2)=4(x1-x2),
∴直线AB的斜率k=
=
,
又直线AB过N(x,y),M(0,3),∴k=
,
∴
=
,整理,得y2-3y-2x=0,
当直线AB的斜率不存在时,上式也成立,
∴AB的中点N的轨迹方程为y2-3y-2x=0.
∴设抛物线的标准方程为y2=2px,p>0,
∵点Q到点F的距离为4,
∴2+p=4,解得p=2,
∴抛物线的标准方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),中点N(x,y),
则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)分别代入y2=4x,得:
|
即2y(y1-y2)=4(x1-x2),
∴直线AB的斜率k=
| y1-y2 |
| x1-x2 |
| 2 |
| y |
又直线AB过N(x,y),M(0,3),∴k=
| y-3 |
| x |
∴
| y-3 |
| x |
| 2 |
| y |
当直线AB的斜率不存在时,上式也成立,
∴AB的中点N的轨迹方程为y2-3y-2x=0.
点评:本题考查抛物线方程的求法,考查抛物线的弦的中点的轨迹方程的求法,是中档题,解题时要注意点差法的合理运用.

练习册系列答案
相关题目
执行如图的程序框图,那么输出的S=( )


| A、720 | B、120 |
| C、24 | D、-120 |
已知三个函数f(x)=2+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则( )
| A、a<b<c |
| B、a<c<b |
| C、b<a<c |
| D、c<a<b |
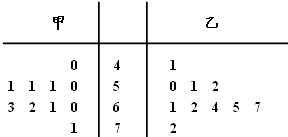 随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图:
随机抽取某中学甲、乙两班各10名学生,测量他们的体重(单位:kg),获得体重数据的茎叶图如图: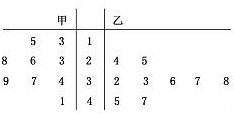 2014年的NBA全明星塞于美国当地时间2014年2月17日在新奥尔良市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
2014年的NBA全明星塞于美国当地时间2014年2月17日在新奥尔良市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )