题目内容
9.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设30多个分支机构,需要国内公司外派大量70后、80后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从70后和80后的员工中随机调查了100位,得到数据如表:| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
(Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排6名参与调查的70后、80后员工参加.70后员工中有愿意被外派的3人和不愿意被外派的3人报名参加,从中随机选出3人,记选到愿意被外派的人数为x;80后员工中有愿意被外派的4人和不愿意被外派的2人报名参加,从中随机选出3人,记选到愿意被外派的人数为y,求x<y的概率.
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (Ⅰ)求出K2,与临界值比较,即可得出结论;
(Ⅱ)利用互斥事件的概率公式,可得结论.
解答 解:(Ⅰ)${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}=\frac{{100×{{(20×20-40×20)}^2}}}{60×40×60×40}$=$\frac{400×400×100}{5760000}≈2.778>2.706$
所以有90% 以上的把握认为“是否愿意被外派与年龄有关”
(Ⅱ)“x<y”包含:“x=0,y=1”、“x=0,y=2”、“x=0,y=3”、“x=1,y=2”、“x=1,y=3”、“x=2,y=3”六个互斥事件
且$P(x=0,y=1)=\frac{C_3^0C_3^3}{C_6^3}×\frac{C_4^1C_2^2}{C_6^3}=\frac{4}{400}$,$P(x=0,y=2)=\frac{C_3^0C_3^3}{C_6^3}×\frac{C_4^2C_2^1}{C_6^3}=\frac{12}{400}$$P(x=0,y=3)=\frac{C_3^0C_3^3}{C_6^3}×\frac{C_4^3C_2^0}{C_6^3}=\frac{4}{400}$,$P(x=1,y=2)=\frac{C_3^1C_3^2}{C_6^3}×\frac{C_4^2C_2^1}{C_6^3}=\frac{108}{400}$$P(x=1,y=3)=\frac{C_3^1C_3^2}{C_6^3}×\frac{C_4^3C_2^0}{C_6^3}=\frac{36}{400}$,$P(x=2,y=3)=\frac{C_3^2C_3^1}{C_6^3}×\frac{C_4^3C_2^0}{C_6^3}=\frac{36}{400}$
所以:$P(x<y)=\frac{4+12+4+108+36+36}{400}=\frac{200}{400}=\frac{1}{2}$.
点评 本题考查独立性检验知识的运用,考查概率的计算,正确计算是关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 25 | 100 | 150 | 155 | 50 | 20 |
| 赞成人数 | 10 | 70 | 120 | 150 | 35 | 15 |
(2)根据用样本估计总体的思想,以样本中事件发生的频率作为相应事件发生的概率,在本市随机采访3人,用X表示3人中对该项措施持赞成态度的人数,求X的分布列和数学期望.
| A. | 110 | B. | 55 | C. | 50 | D. | 不能确定 |
| A. | (2,-2) | B. | (2,2) | C. | (-2,-2) | D. | (-2,2) |
| A. | [$\frac{121}{2}$,81] | B. | [$\frac{121}{2}$,73] | C. | [65,73] | D. | [65,81] |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
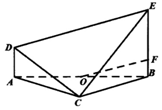 如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.
如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4. 社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.
社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.