题目内容
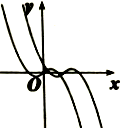
15.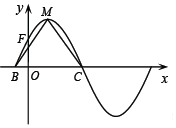 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若f(α-$\frac{π}{4}$)=$\frac{2\sqrt{5}}{5}$,求cos2α的值.
分析 (Ⅰ)依题意,由S△MBC=$\frac{1}{2}$×2×|BC|=|BC|=π可求得其周期T=2π=$\frac{2π}{ω}$,解得ω=1,再由f(0)=2sinφ=$\sqrt{2}$,可求得φ,从而可求函数f(x)的解析式;
(Ⅱ)由f(α-$\frac{π}{4}$)=2sinα=$\frac{2\sqrt{5}}{5}$,可求得sinα,再利用二倍角的余弦即可求得cos2α的值.
解答 解:(Ⅰ)因为S△MBC=$\frac{1}{2}$×2×|BC|=|BC|=π,
所以周期T=2π=$\frac{2π}{ω}$,解得ω=1,
由f(0)=2sinφ=$\sqrt{2}$,得sinφ=$\frac{\sqrt{2}}{2}$,
因为0<φ<$\frac{π}{2}$,所以φ=$\frac{π}{4}$,
所以f(x)=2sin(x+$\frac{π}{4}$);
(Ⅱ)由f(α-$\frac{π}{4}$)=2sinα=$\frac{2\sqrt{5}}{5}$,得sinα=$\frac{\sqrt{5}}{5}$,
所以cos2α=1-2sin2α=$\frac{3}{5}$.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω与φ是关键,考查二倍角的余弦公式的应用,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
4.已知$\overrightarrow a=({sin\frac{ω}{2}x,sinωx}),\overrightarrow b=({sin\frac{ω}{2}x,\frac{1}{2}})$,其中ω>0,若函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$在区间(π,2π)内没有零点,则ω的取值范围是( )
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
5.在等比数列{an}中,若a1=2,a4=16,则{an}的前5项和S5等于( )
| A. | 30 | B. | 31 | C. | 62 | D. | 64 |
 如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
如图ABC-A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.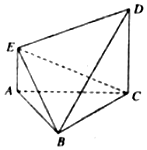 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.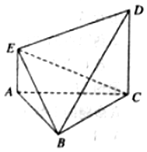 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.