题目内容
7.在平面直角坐标系xOy中,圆C的方程为x2+y2-2x=0(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(2)设直线l的参数方程为$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$(t为参数),若直线l与圆C交于A,B两点,且$|AB|=\sqrt{3}$,求直线l的斜率.
分析 (1)由x=ρcosθ,y=ρsinθ,能求出圆C的极坐标方程.
(2)由直线l的参数方程,求出直线的直角坐标方程,从而能求出直线l的极坐标方程,由|AB|=$\sqrt{3}$,得ρ=$\sqrt{3}$,由此能求出直线l的斜率.
解答 (10分)解:(1)∵圆C的方程为x2+y2-2x=0,
∴由x=ρcosθ,y=ρsinθ,
得圆C的极坐标方程为ρ=2cosθ.…(4分)
(2)∵直线l的参数方程为$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$(t为参数),
∴直线的直角坐标方程为y=tanα•x,
∴直线l的极坐标方程为θ=α(ρ∈R)…(6分)
∵|AB|=$\sqrt{3}$,∴ρ=$\sqrt{3}$,
∴cosα=$\frac{\sqrt{3}}{2}$,…(9分)
∴tanα=$±\frac{\sqrt{3}}{3}$,
∴直线l的斜率为$±\frac{\sqrt{3}}{3}$.…(10分)
点评 本题考查圆的极坐标方程、直线的斜率的求法,考查直角坐标方程、极坐标方程、参数方程的互化及应用,考查推导论证能力、数据得理能力,考查数形结合思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
 已知如图是一个空间几何体的三视图.
已知如图是一个空间几何体的三视图.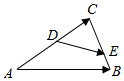 如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.
如图,D,E分别是△ABC的边AC,BC上的点,且$\overrightarrow{AD}$=$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{EC}$.若$\overrightarrow{DE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$(λ,μ∈R),则λ+μ的值为$\frac{1}{2}$.