题目内容
8.已知$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3$,向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$,则$\vec a•(\vec a-\vec b)$的值为( )| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
分析 根据数量积定义计算$\overrightarrow{a}•\overrightarrow{b}$,再将$\vec a•(\vec a-\vec b)$展开计算.
解答 解:$\overrightarrow{a}•\overrightarrow{b}$=2×3×cos$\frac{π}{3}$=3,
${\overrightarrow{a}}^{2}$=4,
∴$\vec a•(\vec a-\vec b)$=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=4-3=1.
故选A.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
17.复数($\frac{1-ai}{a+i}$)2017=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |

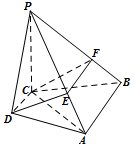 如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F.
如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F. 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.