题目内容
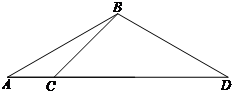
 如图,在△ABC中,∠ACB为钝角,AB=2,BC=
如图,在△ABC中,∠ACB为钝角,AB=2,BC=| 2 |
| π |
| 6 |
| 3 |
(Ⅰ)求∠BCD的大小;
(Ⅱ)求BD的长及△ABC的面积.
考点:余弦定理的应用
专题:解三角形
分析:(Ⅰ)利用正弦定理求出∠BCD的正弦函数值,然后求出角的大小;
(Ⅱ)在△BCD中,由余弦定理可求BD的长,然后求出AC的长,即可求解△ABC的面积.
(Ⅱ)在△BCD中,由余弦定理可求BD的长,然后求出AC的长,即可求解△ABC的面积.
解答:
 (本小题满分13分)
(本小题满分13分)
解:(Ⅰ)在△ABC中,
因为AB=2,A=
,BC=
,
由正弦定理可得
=
,
即
=
=
=2
,
所以sin∠ACB=
.
因为∠ACB为钝角,所以∠ACB=
.
所以∠BCD=
. …(6分)
(Ⅱ)在△BCD中,由余弦定理可知BD2=CB2+DC2-2CB•DC•cos∠BCD,
即BD2=(
)2+(
+1)2-2•
•(
+1)•cos
,
整理得BD=2.
在△ABC中,由余弦定理可知BC2=AB2+AC2-2AB•AC•cosA,
即(
)2=22+AC2-2•2•AC•cos
,
整理得AC2-2
AC+2=0.解得AC=
±1.
因为∠ACB为钝角,所以AC<AB=2.所以AC=
-1.
所以△ABC的面积S=
AC•AB•sinA=
×2×(
-1)×
=
.….(13分)
 (本小题满分13分)
(本小题满分13分)解:(Ⅰ)在△ABC中,
因为AB=2,A=
| π |
| 6 |
| 2 |
由正弦定理可得
| AB |
| sin∠ACB |
| BC |
| sinA |
即
| 2 |
| sin∠ACB |
| ||
sin
|
| ||
|
| 2 |
所以sin∠ACB=
| ||
| 2 |
因为∠ACB为钝角,所以∠ACB=
| 3π |
| 4 |
所以∠BCD=
| π |
| 4 |
(Ⅱ)在△BCD中,由余弦定理可知BD2=CB2+DC2-2CB•DC•cos∠BCD,
即BD2=(
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
整理得BD=2.
在△ABC中,由余弦定理可知BC2=AB2+AC2-2AB•AC•cosA,
即(
| 2 |
| π |
| 6 |
整理得AC2-2
| 3 |
| 3 |
因为∠ACB为钝角,所以AC<AB=2.所以AC=
| 3 |
所以△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查余弦定理的应用,解三角形,考查基本知识的应用.

练习册系列答案
相关题目
集合{a,b}的子集个数为( )
| A、4 | B、3 | C、2 | D、1 |
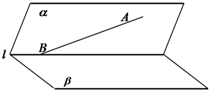 如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是