题目内容
若数列{an}满足
=
,a1=1,则a6=( )
| 1 |
| an+1 |
| 2an+1 |
| an |
A、
| ||
B、
| ||
| C、10 | ||
| D、11 |
考点:数列递推式
专题:等差数列与等比数列
分析:根据数列的递推关系,得到数列{
}是等差数列.即可得到结论.
| 1 |
| an |
解答:
解:∵数列{an}满足
=
=2+
,
即
-
=2,
即数列{
}是等差数列,公差d=2.首项为1,
则
=1+5×2=11,
则a6=
,
故选:A
| 1 |
| an+1 |
| 2an+1 |
| an |
| 1 |
| an |
即
| 1 |
| an+1 |
| 1 |
| an |
即数列{
| 1 |
| an |
则
| 1 |
| a6 |
则a6=
| 1 |
| 11 |
故选:A
点评:本题主要考查数列的项的计算,根据条件构造等差数列是解决本题的关键.

练习册系列答案
相关题目
若P(A)=
,P(B|A)=
,则P(AB)等于( )
| 9 |
| 10 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a=
-
,b=
-3,c=
,则a,b,c的大小关系为( )
| 7 |
| 5 |
| 11 |
| ||
| 10 |
| A、a<b<c |
| B、b<a<c |
| C、c<a<b |
| D、c<b<a |
已知y=f(x)在R上可导,且f(1)=2,若f′(x)>2,则不等式f(x)>2x的解集为( )
| A、(-∞,1) |
| B、(1,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |
在数列{an}中,a1=1,an+1=2an+3,则a9的值为( )
| A、512 | B、511 |
| C、1024 | D、1021 |
“m=2”是“直线3x+(m+1)y-(m-7)=0与直线mx+2y+3m=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设0<α<β<
,cosα+sinα=a,cosβ+sinβ=b,则( )
| π |
| 4 |
| A、a<b | B、a>b |
| C、ab<1 | D、ab>2 |
方程x2cosα+y2sinα=1表示焦点在y轴上的双曲线,则α是第( )象限角.
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
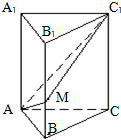 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=