题目内容
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),已知过点P(-2,-4)的直线l的参数方程为
,直线l与曲线C分别交于M,N.
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
|
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
考点:直线的参数方程
专题:坐标系和参数方程
分析:(1)利用极坐标化为直角坐标方程的公式x=ρcosθ,y=ρsinθ可得曲线C的方程;消去参数t即可得到直线l的方程;
(2)把直线的方程代入抛物线的方程得到根与系数的关系,利用两点间的距离公式和等比数列的定义即可得出.
(2)把直线的方程代入抛物线的方程得到根与系数的关系,利用两点间的距离公式和等比数列的定义即可得出.
解答:
解:(1)由曲线C:ρsin2θ=2acosθ(a>0),可得ρ2sin2θ=2aρcosθ,化为y2=2ax.
由直线l的参数方程为
,消去参数t可得直线l:y=x-2.
(2)联立
,
化为x2-(4+2a)x+4=0,
∵直线l与抛物线相交于两点,
∴△=(4+2a)2-16>0,解得a>0或a<-4.(*)
∴x1+x2=4+2a,x1x2=4.
∴|MN|=
=
=
.
|PM|=
=
|x1+2|,|PN|=
|x2+2|.
∴|PM||PN|=2|(x1+2)(x2+2)|=2|x1x2+2(x1+x2)+4|
=2|16+4a|
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM||PN|,
∴(
)2=2|16+4a|,
化为a(4+a)=|4+a|,
∵a>0或a<-4.
解得a=1.
∴a=1.
由直线l的参数方程为
|
(2)联立
|
化为x2-(4+2a)x+4=0,
∵直线l与抛物线相交于两点,
∴△=(4+2a)2-16>0,解得a>0或a<-4.(*)
∴x1+x2=4+2a,x1x2=4.
∴|MN|=
| (1+1)[(x1+x2)2-4x1x2] |
| 2[(4+2a)2-16] |
| 8a2+32a |
|PM|=
| (x1+2)2+(y1+4)2 |
| 2 |
| 2 |
∴|PM||PN|=2|(x1+2)(x2+2)|=2|x1x2+2(x1+x2)+4|
=2|16+4a|
∵|PM|,|MN|,|PN|成等比数列,
∴|MN|2=|PM||PN|,
∴(
| 8a2+32a |
化为a(4+a)=|4+a|,
∵a>0或a<-4.
解得a=1.
∴a=1.
点评:本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与抛物线相交问题转化为把直线的方程与抛物线的方程联立得到根与系数的关系、两点间的距离公式和等比数列的定义等基础知识与基本技能方法,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={x||x+1|<1},B={x|y=
,y∈R},则A∩∁RB=( )
(
|
| A、(-2,1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
 如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=
如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=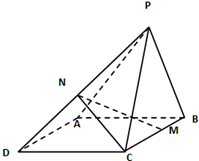 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.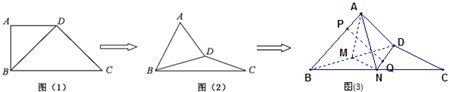 在直角梯形ABCD中,AD∥BC,
在直角梯形ABCD中,AD∥BC,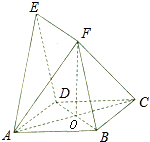 如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2
如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2