题目内容
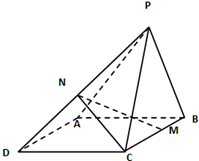 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,AB=2,△PCB为正三角形,且平面PCB⊥平面ABCD,M,N分别为BC,PD的中点.(1)求证:MN∥面APB;
(2)求二面角B-NC-P的余弦值;
(3)求四棱锥P-ABCD被截面MNC分成的上下两部分体积之比.
考点:与二面角有关的立体几何综合题,组合几何体的面积、体积问题,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取AD中点O,连接MO,NO,由已知条件推导出四边形ABCD为平行四边形,由此能够证明MN∥面PAB.
(2)建立空间直角坐标系,利用向量法能求出二面角B-NC-P的余弦值.
(3)利用向量法求出点P到平面MNC的距离,由棱锥体积的计算公式能求出四棱锥P-ABCD被截面MNC分成的上下两部分体积之比.
(2)建立空间直角坐标系,利用向量法能求出二面角B-NC-P的余弦值.
(3)利用向量法求出点P到平面MNC的距离,由棱锥体积的计算公式能求出四棱锥P-ABCD被截面MNC分成的上下两部分体积之比.
解答:
(1)证明:取AD中点O,连接MO,NO,
∵M,N分别为DE,PB的中点,
∴ON∥PA,ON∥面PAB
又∵四边形ABCD为平行四边形,
∴OM∥AB,∵OM在平面PAB外,AB?平面PAB,
∴OM∥面PAB,
∵面MON∥面PAB,∴MN∥面PAB.(3分)
(2)建立空间直角坐标系如图,
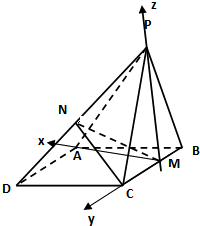 由题意知:P(0,0,
由题意知:P(0,0,
),A(
,0,0),B(0,-1,0),
C(0,1,0),D(
,2,0),
∵N为PD中点,∴N(
,1,
),(4分)
∴
=(
,1,-
),
=(0,1,-
),
=(
,2,
),
=(0,2,0),
令平面PNC的法向量
=(x, y, z),
∵
•
=0,
•
=0,
∴
,∴
=(-1,
, 1).
设平面BNC的法向量
=(
,y1,z1),
∵
•
=0,
•
=0,
∴
,∴
=(1,0,-1),(6分)
∴cos<
,
>=
=-
,
∵二面角B-NC-P的平面角为锐角,
∴二面角B-NC-P的余弦值为
.(8分)
(3)∵
=(0,0,
),平面MNC的法向量为
=(1,0,-1),
∴点P到平面MNC的距离d=|
|=|
|=
,
设PA中点为E,则NE=1,BC=2,
=(0,2,0),
=(
,0,
),
∴
•
=0,|
|=
,
∴直角梯形ENCB的面积为
(1+2)×
=
,
∴V上=
×
×
=
V下=
×2
×
-
=
,
∴
=
,
∴四棱锥P-ABCD被截面MNC分成的上下两部分体积之比为
.(12分)
∵M,N分别为DE,PB的中点,
∴ON∥PA,ON∥面PAB
又∵四边形ABCD为平行四边形,
∴OM∥AB,∵OM在平面PAB外,AB?平面PAB,
∴OM∥面PAB,
∵面MON∥面PAB,∴MN∥面PAB.(3分)
(2)建立空间直角坐标系如图,
 由题意知:P(0,0,
由题意知:P(0,0,| 3 |
| 3 |
C(0,1,0),D(
| 3 |
∵N为PD中点,∴N(
| ||
| 2 |
| ||
| 2 |
∴
| PN |
| ||
| 2 |
| ||
| 2 |
| PC |
| 3 |
| BN |
| ||
| 2 |
| ||
| 2 |
| BC |
令平面PNC的法向量
| n |
∵
| n |
| PN |
| n |
| PC |
∴
|
| n |
| 3 |
设平面BNC的法向量
| m |
| x | 1 |
∵
| m |
| BN |
| m |
| BC |
∴
|
| m |
∴cos<
| m |
| n |
| -1+0-1 | ||||
|
| ||
| 5 |
∵二面角B-NC-P的平面角为锐角,
∴二面角B-NC-P的余弦值为
| ||
| 5 |
(3)∵
| MP |
| 3 |
| m |
∴点P到平面MNC的距离d=|
| ||||
|
-
| ||
|
| ||
| 2 |
设PA中点为E,则NE=1,BC=2,
| BC |
| CN |
| ||
| 2 |
| ||
| 2 |
∴
| BC |
| CN |
| CN |
| ||
| 2 |
∴直角梯形ENCB的面积为
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
∴V上=
| 1 |
| 3 |
3
| ||
| 4 |
| ||
| 2 |
| 3 |
| 4 |
V下=
| 1 |
| 3 |
| 3 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
∴
| V上 |
| V下 |
| 3 |
| 5 |
∴四棱锥P-ABCD被截面MNC分成的上下两部分体积之比为
| 3 |
| 5 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,考查棱锥体积的计算,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
条件p:-2<x<4,条件q:(x+2)(x+a)<0;若p是q的充分而不必要条件,则a的取值范围是( )
| A、(4,+∞) |
| B、(-∞,-4) |
| C、(-∞,-4] |
| D、[-4,+∞) |
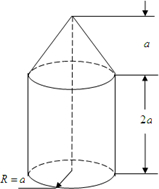 图示是一个几何体的直观图,画出它的三视图.
图示是一个几何体的直观图,画出它的三视图.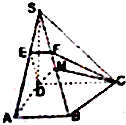 在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=