题目内容
7．如果满足∠A=60°，BC=6，AB=k的锐角△ABC有且只有一个，那么实数k的取值范围是$（2\sqrt{3}，4\sqrt{3}）$．分析 依题意，可得C大于30°且小于90°，结合正弦定理解之即可．
解答 解：由题意，30°＜C＜90°，∴$\frac{1}{2}$＜sinC＜1
由正弦定理可得$\frac{k}{sinC}$=$\frac{6}{\frac{\sqrt{3}}{2}}$，
∴k=4$\sqrt{3}$sinC
∴k∈$（2\sqrt{3}，4\sqrt{3}）$，
故答案为$（2\sqrt{3}，4\sqrt{3}）$．
点评 本题考查正弦定理的运用，考查特殊角的三角函数，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
14．阅读程序框图，运行相应的程序，则输出s的值为（ ）
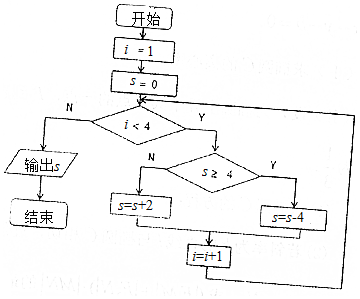
| A． | 0 | B． | 2 | C． | 4 | D． | 6 |
18．$（a+\frac{1}{x}）{（1+x）^4}$展开式中x2的系数为0，则a=（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{3}{2}$ | D． | $-\frac{3}{2}$ |
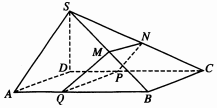已知四棱锥S-ABCD的底面为平行四边形，且SD⊥平面ABCD，AB=2AD=2SD，∠DCB=60°，M，N分别为SB，SC的中点，过MN作平面MNPQ分别与线段CD，AB相交于P，Q两点（不与A，B重合）．
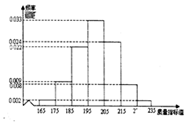从某企业的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：