题目内容
18.$(a+\frac{1}{x}){(1+x)^4}$展开式中x2的系数为0,则a=( )| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
分析 把(1+x)4按照二项式定理展开,即可求得$(a+\frac{1}{x}){(1+x)^4}$的展开式中x2的系数,再根据展开式中x2的系数为0,求得实数a的值.
解答 解:∵$(a+\frac{1}{x}){(1+x)^4}$=(a+$\frac{1}{x}$)(1+4x+6x2+4x3+x4 ),
∴展开式中x2的系数为6a+4=0,求得a=-$\frac{2}{3}$,
故选B.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
5.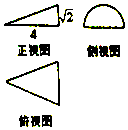 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
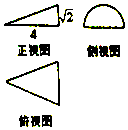 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{4}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | 4π | D. | 4$\sqrt{2}$π |