题目内容
13.已知函数y=$\frac{lnx}{x}$在点(m,f(m))处的切线平行于x轴,则实数m=e.分析 求出函数的导数,可得切线的斜率,再由两直线平行的条件:斜率相等,可得m的方程,解方程即可得到所求值.
解答 解:由函数y=$\frac{lnx}{x}$,得导数f′(x)=$\frac{1-lnx}{{x}^{2}}$,
可得切线的斜率为k=$\frac{1-lnm}{{m}^{2}}$,
由切线平行于x轴,可得k=$\frac{1-lnm}{{m}^{2}}$=0,
得1-lnm=0,即m=e,
故答案为:e.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,以及两直线平行的条件:斜率相等,考查运算能力,属于基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
3.在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 语文成绩x | 60 | 70 | 74 | 90 | 94 | 110 |
| 历史成绩y | 58 | 63 | 75 | 79 | 81 | 88 |
(2)用上表数据画出散点图易发现历史成绩y与语文成绩x具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.1).参考公式:回归直线方程是y=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$.
1.若集合A={-2,-1,0,1,2},集合B={x|x(x+3)<0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-2,-1} | C. | {1,2} | D. | {0,1,2} |
8.下列命题中正确的是( )
| A. | 若α>β,则sinα>sinβ | |
| B. | 命题:“?x>1,x2>1”的否定是“?x≤1,x2≤1” | |
| C. | 已知函数f(x)=x3+ax2+bx+c,若f(x)在区间(-1,0)上单调递减,则a2+b2的取值范围为$[{\frac{9}{5},+∞})$ | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
18.给出下列四个结论,其中一定正确的是( )
| A. | $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}$ | B. | $\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BD}$ | C. | $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ | D. | $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}$ |
5.在直角坐标系xOy中,圆M的参数方程为$\left\{\begin{array}{l}{x=1+2cost}\\{y=-2+2sint}\end{array}\right.$(t为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程为$\sqrt{2}$ρsin(θ-$\frac{π}{4}$)=m,(m∈R),若直线l与圆M相交于A,B两点,△MAB的面积为2,则m值为( )
| A. | -1或3 | B. | 1或5 | C. | -1或-5 | D. | 2或6 |
17.为了了解青少年的肥胖情况是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
(3)若这30名青少年中,常喝碳酸饮料且肥胖的有2名女生,则从常喝碳酸饮料且肥胖的青少年中随机抽取2名,恰好抽到一男一女的概率是多少?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a-b)(c+d)(a-c)(b+d)}$,其中n=a+b+c+d)
| 常喝 | 不常喝 | 总计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 总计 | 30 |
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
(3)若这30名青少年中,常喝碳酸饮料且肥胖的有2名女生,则从常喝碳酸饮料且肥胖的青少年中随机抽取2名,恰好抽到一男一女的概率是多少?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a-b)(c+d)(a-c)(b+d)}$,其中n=a+b+c+d)
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
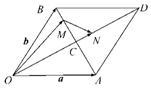 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,试用a,b表示$\overrightarrow{OM}$,$\overrightarrow{ON}$,$\overrightarrow{MN}$.