题目内容
6.已知(a-i)2=-2i,其中i是虚数单位,a是实数,则|ai|=( )| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
分析 利用复数的运算法则、复数相等、模的计算公式即可得出.
解答 解:(a-i)2=-2i,其中i是虚数单位,a是实数,
∴a2-1-2ai=-2i,∴a2-1=0,-2a=-2,∴a=1.
则|ai|=|i|=1.
故选:B.
点评 本题考查了复数的运算法则、复数相等、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1右焦点为F,P为双曲线左支点上一点,点A(0,$\sqrt{2}$),则△APF周长的最小值为( )
| A. | 4(1+$\sqrt{2}$) | B. | 4+$\sqrt{2}$ | C. | 2($\sqrt{2}$+$\sqrt{6}$) | D. | $\sqrt{6}$+3$\sqrt{2}$ |
17.要计算1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2017}$的结果,如图程序框图中的判断框内可以填( )

| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为2,离心率为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{16}$=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{2}$$-\frac{{y}^{2}}{3}$=1 | D. | x2$-\frac{{y}^{2}}{6}$=1 |
1.阅读如图所示的程序框图,运行相应的程序,则输出i的值为( )
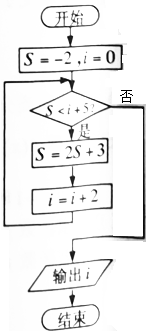

| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
11.执行如图所示的程序框图,若输入的a,b分别为36,28,则输出的a=( )


| A. | 4 | B. | 8 | C. | 12 | D. | 20 |
18.已知m,n是两条不同的直线,α是平面,则下列命题中是真命题的是( )
| A. | 若m∥α,m∥n,则n∥α | B. | 若m⊥α,n⊥α,则m∥n | C. | 若m∥α,m⊥n,则n∥α | D. | 若m⊥α,n⊥m,则n∥α |