题目内容
经过原点且与函数y=ex(e为自然对数的底数)的图象相切的直线方程为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:根据函数f(x)的解析式设出切点的坐标,根据设出的切点坐标和原点求出切线的斜率,同时由f(x)求出其导函数,把切点的横坐标代入导函数中即可表示出切线的斜率,两次求出的斜率相等列出关于a的方程,求出方程的解即可得到a的值,进而得到切点坐标,根据切点坐标和切线过原点写出切线方程即可.
解答:
解:设切点坐标为(a,ea),
又切线过(0,0),得到切线的斜率k=
,
又f′(x)=ex,把x=a代入得:斜率k=f′(a)=ea,
则ea=
,由于ea>0,则得到a=1,
即切点坐标为(1,e),
所以切线方程为:y=ex.
故答案为:y=ex.
又切线过(0,0),得到切线的斜率k=
| ea |
| a |
又f′(x)=ex,把x=a代入得:斜率k=f′(a)=ea,
则ea=
| ea |
| a |
即切点坐标为(1,e),
所以切线方程为:y=ex.
故答案为:y=ex.
点评:此题考查学生会利用导数求曲线上过某点切线方程,注意要区别在某点处的切线,解题的关键是确定切点,本题是一道基础题.

练习册系列答案
相关题目
下列程序语句的算法功能是( )
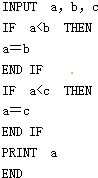
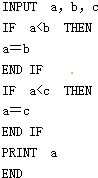
| A、输出a,b,c三个数中的最大数 |
| B、输出a,b,c三个数中的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
已知i为虚数单位,则|1-2i|=( )
| A、1 | ||
| B、2 | ||
| C、-2 | ||
D、
|
设集合M={x|-1<x<1},N={x|x2≤x},则M∩N=( )
| A、[0,1) |
| B、(-1,1] |
| C、[-1,1) |
| D、(-1,0] |
不等式组
在坐标平面内表示的图形的面积等于( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
