题目内容
角A、B、C为△ABC的三个内角,且角B满足sinB+cos(B+
)=
.
(1)求角B的值;
(2)若sinA+sinC>k恒成立,试求实数k的取值范围.
| π |
| 6 |
| ||
| 2 |
(1)求角B的值;
(2)若sinA+sinC>k恒成立,试求实数k的取值范围.
考点:三角函数中的恒等变换应用
专题:三角函数的求值,解三角形
分析:(1)通过两角和公式对已知等式整理求得sin(B+
)的值,进而根据B的范围求得B+
,进而求得B.
(2)利用(1)中B的值,表示出C,利用两角和公式化简整理,进而利用A的范围求得sinA+sinC的范围,最后求得k.
| π |
| 3 |
| π |
| 3 |
(2)利用(1)中B的值,表示出C,利用两角和公式化简整理,进而利用A的范围求得sinA+sinC的范围,最后求得k.
解答:
解:(1)sinB+cos(B+
)=sinB+
cosB-
sinB=
sinB+
cosB=sin(B+
)=
.
∵0<B<π,
∴
<B+
<
,
∴B+
=
,B=
.
(2)∵A+B+C=π,
∴C=
-A∈(0,
),
∴sinA+sinC=sinA+sin(
-A)=
sinA+
cosA=
sin(A+
),
∵A+
∈(
,
),
∴sin(A+
)∈(
,1],
∴
sin(A+
)∈(
,
],
∴要使sinA+sinC>k恒成立,则k≤
.
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∵0<B<π,
∴
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴B+
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
(2)∵A+B+C=π,
∴C=
| 2π |
| 3 |
| 2π |
| 3 |
∴sinA+sinC=sinA+sin(
| 2π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 6 |
∵A+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(A+
| π |
| 6 |
| 1 |
| 2 |
∴
| 3 |
| π |
| 6 |
| ||
| 2 |
| 3 |
∴要使sinA+sinC>k恒成立,则k≤
| ||
| 2 |
点评:本题要考查了三角函数恒等变换的应用,三角函数图象和性质.解题的过程中要特别关注三角形中角的隐含范围,例如本题中C的范围.

练习册系列答案
相关题目
复数
(i为虚数单位)的模为( )
| 2+i |
| i |
A、
| ||
| B、±(1-2i) | ||
C、
| ||
| D、1-2i |
某几何体的三视图如图所示,则该几何体的表面积为( )
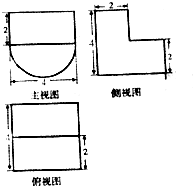

| A、40+12π |
| B、16+8π |
| C、16+16π |
| D、16+32π |