题目内容
3.设f(x)=$\left\{\begin{array}{l}{2{e}^{x-1}(x<2)}\\{\frac{1}{2}+lnx(x≥2)}\end{array}\right.$,则f(f(e))的值为( )| A. | 0 | B. | $\sqrt{e}$ | C. | 2$\sqrt{e}$ | D. | 3 |
分析 利用分段函数的性质求解.
解答 解:∵f(x)=$\left\{\begin{array}{l}{2{e}^{x-1}(x<2)}\\{\frac{1}{2}+lnx(x≥2)}\end{array}\right.$,
∴f(e)=$\frac{1}{2}+lne$=$\frac{3}{2}$,
f(f(e))=f($\frac{3}{2}$)=$2{e}^{\frac{3}{2}-1}$=2$\sqrt{e}$.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数性质的合理运用.

练习册系列答案
相关题目
14.数列{an}满足a1=2,${a_{n+1}}=\frac{1}{{1-{a_n}}}(n∈{N^*})$,则a2016=( )
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
15.若cosθ=$\frac{3}{5}$(-$\frac{π}{2}$<θ<0),则cos(θ-$\frac{π}{6}$)的值是( )
| A. | $\frac{3\sqrt{3}±4}{10}$ | B. | $\frac{4±3\sqrt{3}}{10}$ | C. | $\frac{3\sqrt{3}-4}{10}$ | D. | $\frac{3\sqrt{3}+4}{10}$ |
12.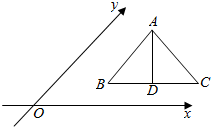 如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
 如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )
如图所示的是水平放置的三角形的直观图,D为△ABC中BC的中点,则原图形中的AB,AD,AC三条线段中( )| A. | 最长的是AB,最短的是AC | B. | 最长的是AC,最短的是AB | ||
| C. | 最长的是AB,最短的是AD | D. | 最长的是AC,最短的是AD |
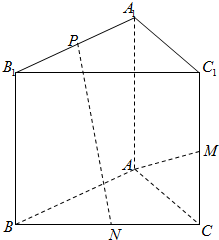 已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.
已知如图,在直三棱柱ABC-A1B1C1中,AA1=AC,且AB⊥AC,M是面CC1的中点,N是BC的中点,点P在直线A1B1上.


