题目内容
从圆C:(x-1)2+(y-1)2=1外一点p(-2,3),向圆C引切线,切点为M、N.
(1)求切线方程;
(2)求过二切点的直线方程.
(1)求切线方程;
(2)求过二切点的直线方程.
考点:圆的切线方程
专题:计算题,直线与圆
分析:(1)设切线方程为y=k(x+2)+3,利用圆心到直线的距离等于半径,即可求切线方程;
(2)求出四边形PMCN外接圆方程,即可求过二切点的直线方程.
(2)求出四边形PMCN外接圆方程,即可求过二切点的直线方程.
解答:
解:(1)设切线方程为y=k(x+2)+3,即kx-y+2k+3=0⇒
=1⇒k=
或k=-
故所求切线方程为:(
+6)x-4y+2
-3=0或(3+
)x+4y-6+2
=0
(2)C、P中点坐标(-
,2),|PC|=5,
故四边形PMCN外接圆方程为(x+
)2+(y-2)2=
,即x2+y2+x-4y-2=0
与圆C:(x-1)2+(y-1)2=1相减可得过二切点M、N的直线方程为3x-2y-3=0.
| |3k+2| | ||
|
-3+
| ||
| 4 |
3+
| ||
| 4 |
故所求切线方程为:(
| 3 |
| 3 |
| 3 |
| 3 |
(2)C、P中点坐标(-
| 1 |
| 2 |
故四边形PMCN外接圆方程为(x+
| 1 |
| 2 |
| 25 |
| 4 |
与圆C:(x-1)2+(y-1)2=1相减可得过二切点M、N的直线方程为3x-2y-3=0.
点评:本题考查圆的切线方程,考查圆与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(x-y,x+y),则与B中的元素(-1,1)对应的A中的元素为( )
| A、(0,1) |
| B、(1,3) |
| C、(-1,-3) |
| D、(-2,0) |
函数f(x)=
是奇函数,则常数a的值是( )
| x+a |
| x2+1 |
| A、0 | B、1 | C、-1 | D、任意实数 |
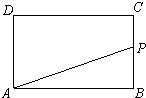 如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).
如图,在长为4、宽为2的矩形ABCD上有一点P,沿折线BCDA由B点(起点)向A点(终点)移动,设P点移动的路程为x,△ABP的面积为y=f(x).