题目内容
函数f（x）=
是奇函数，则常数a的值是（ ）
| x+a |
| x2+1 |
| A、0 | B、1 | C、-1 | D、任意实数 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：直接利用奇函数的定义求出a的值即可．
解答：
解：函数f（x）=
是奇函数，
∴
=-
，
即-x+a=-x-a，
可得a=0．
故选A．
| x+a |
| x2+1 |
∴
| -x+a |
| (-x)2+1 |
| x+a |
| x2+1 |
即-x+a=-x-a，
可得a=0．
故选A．
点评：本题考查函数的奇偶性的应用，考查计算能力．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
在公比为整数的等比数列{an}中，若，a1+a3=6，a2+a4=12，则a3等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
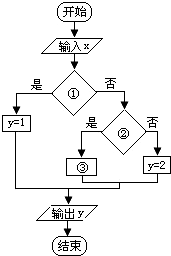任给x的值，计算函数y=
|
| A、x＜1、x＞1、y=3 |
| B、x=1、x＞1、y=3 |
| C、x＜1、x=1、y=3 |
| D、x＜1、x＞1、y=3 |