题目内容

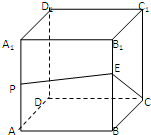已知正方体ABCD-A1B1C1D1的棱长为2，P是AA1的中点，E是BB1上的点，则PE+EC的最小值是
 
．
考点：多面体和旋转体表面上的最短距离问题
专题：综合题,空间位置关系与距离
分析：根据题意可得：可以把平面BCC1B1展开，根据图象可得若PE+EC取最小值，则P，E，C三点共线，可得PE+EC的最小值为PC的长度，再结合题意求出答案即可．
解答： 解：根据题意可得：可以把平面BCC1B1展开，如图所示，

若PE+EC取最小值，则P，E，C三点共线，
∴PE+EC的最小值为PC，
∵正方体ABCD-A1B1C1D1的棱长为2，P是AA1的中点，
∴|PC|=
12+42
=
17
．
故答案为：
17
．
点评：本题主要考查空间中点之间的距离，解决此题的关键是能够把空间问题转化为平面问题．
练习册系列答案
相关题目
数列{an}的前n和为Sn，且满足an+Sn=1（n∈N*）
（1）求数列{an}的通项公式；
（2）是否存在实数λ，使得数列{Sn+λn+
3λ
2n
}为等差数列，若存在，求出λ的值，若不存在，说明理由；
（3）设bn=
1
2n+1(an+1)(an+1+1)
，求数列{bn}的前n项和Tn．
已知数列{an}满足a1=1，且各项均不等于零，an+1+2anan+1-an=0，（n∈N*）
（1）求证数列{
1
an
}是等差数列；
（2）若a1a2+a2a3+a3a4+…+anan+1＞
21
43
，求n的取值范围．
设计一个算法，根据输入x的值，计算y=
3x-1x≥1
1-3xx＜1
的值，写其程序并画出其流程图．
已知等差数列{an}的首项为10，公差为2，等比数列{bn}的首项为1，公比为2，n∈N*．
（1）求数列{an}与{bn}的通项公式；
（2）设第n个正方形的边长为Cn=min{an，bn}，求前n个正方形的面积之和Sn．（注：min{a，b}表示a与b的最小值．）
在平面直角坐标系上，设不等式组
x＞0
y＞0
y≤-n(x-3)
所表示的平面区域为Dn，记Dn内的整点（即横坐标和纵坐标均为整数的点）的个数为an（n∈N*）．则a1=
 
，经推理可得到an=
 
．
已知P（x，y）满足
x≤1
y≥1
x-2y+3≥0
，则点P到直线3x-4y-9=0的距离的最小值为
 
．
已知变量x，y满足
2x-y≤0
x-2y+3≥0
x≥0
，则2x+y的最大值为
 
．
复数1+
3
i与复数-
3
+i在复平面上的对应点分别是A，B，O为坐标，则∠AOB等于（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网