题目内容
已知等差数列{an}的首项为10,公差为2,等比数列{bn}的首项为1,公比为2,n∈N*.
(1)求数列{an}与{bn}的通项公式;
(2)设第n个正方形的边长为Cn=min{an,bn},求前n个正方形的面积之和Sn.(注:min{a,b}表示a与b的最小值.)
(1)求数列{an}与{bn}的通项公式;
(2)设第n个正方形的边长为Cn=min{an,bn},求前n个正方形的面积之和Sn.(注:min{a,b}表示a与b的最小值.)
考点:数列的应用
专题:综合题,等差数列与等比数列
分析:(1)直接利用等差数列、等比数列的通项公式,即可求数列{an}与{bn}的通项公式;
(2)先证明当n≥6时,不等式bn>an成立,再用分组求和法,求出前n个正方形的面积之和Sn.
(2)先证明当n≥6时,不等式bn>an成立,再用分组求和法,求出前n个正方形的面积之和Sn.
解答:
解:(1)因为等差数列{an}的首项为10,公差为2,
所以an=10+(n-1)×2,即an=2n+8.
因为等比数列{bn}的首项为1,公比为2,
所以bn=1×2n-1,即bn=2n-1.
(2)因为a1=10,a2=12,a3=14,a4=16,a5=18,a6=20,b1=1,b2=2,b3=4,b4=8,b5=16,b6=32.
易知当n≤5时,an>bn.
下面证明当n≥6时,不等式bn>an成立.
方法1:①当n=6时,b6=26-1=32>20=2×6+8=a6,不等式显然成立.
②假设当n=k(k≥6)时,不等式成立,即2k-1>2k+8.
则有2k=2×2k-1>2(2k+8)=2(k+1)+8+(2k+6)>2(k+1)+8.
这说明当n=k+1时,不等式也成立.
综合①②可知,不等式对n≥6的所有整数都成立.
所以当n≥6时,bn>an.
方法2:因为当n≥6时bn-an=2n-1-(2n+8)=(1+1)n-1-(2n+8)=(
+
+
+…+
)-(2n+8)≥(
+
+
+
+
+
)-(2n+8)
=2(
+
+
)-(2n+8)=n2-3n-6=n(n-4)+(n-6)>0,
所以当n≥6时,bn>an.
所以n≤5时,Sn=c12+c22+c32+…+cn2=b12+b22+b32+…+bn2
=20+22+24+…+22n-2=
=
(4n-1).
当n>5时,Sn=c12+c22+c32+…+cn2
=(b12+b22+…+b52)+(a62+a72+…+an2)=
(45-1)+4[(6+4)2+(7+4)2+…+(n+4)2]
=341+4[(62+72+…+n2)+8(6+7+…+n)+16(n-5)]
=341+4[(12+22+…+n2)-(12+22+…+52)]+32(6+7+…+n)+64(n-5)
=341+4[
-55]+32×
+64(n-5)=
n3+18n2+
n-679.
综上可知,Sn=
所以an=10+(n-1)×2,即an=2n+8.
因为等比数列{bn}的首项为1,公比为2,
所以bn=1×2n-1,即bn=2n-1.
(2)因为a1=10,a2=12,a3=14,a4=16,a5=18,a6=20,b1=1,b2=2,b3=4,b4=8,b5=16,b6=32.
易知当n≤5时,an>bn.
下面证明当n≥6时,不等式bn>an成立.
方法1:①当n=6时,b6=26-1=32>20=2×6+8=a6,不等式显然成立.
②假设当n=k(k≥6)时,不等式成立,即2k-1>2k+8.
则有2k=2×2k-1>2(2k+8)=2(k+1)+8+(2k+6)>2(k+1)+8.
这说明当n=k+1时,不等式也成立.
综合①②可知,不等式对n≥6的所有整数都成立.
所以当n≥6时,bn>an.
方法2:因为当n≥6时bn-an=2n-1-(2n+8)=(1+1)n-1-(2n+8)=(
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-1 n-1 |
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
| C | n-3 n-1 |
| C | n-2 n-1 |
| C | n-1 n-1 |
=2(
| C | 0 n-1 |
| C | 1 n-1 |
| C | 2 n-1 |
所以当n≥6时,bn>an.
所以n≤5时,Sn=c12+c22+c32+…+cn2=b12+b22+b32+…+bn2
=20+22+24+…+22n-2=
| 1-4n |
| 1-4 |
| 1 |
| 3 |
当n>5时,Sn=c12+c22+c32+…+cn2
=(b12+b22+…+b52)+(a62+a72+…+an2)=
| 1 |
| 3 |
=341+4[(62+72+…+n2)+8(6+7+…+n)+16(n-5)]
=341+4[(12+22+…+n2)-(12+22+…+52)]+32(6+7+…+n)+64(n-5)
=341+4[
| n(n+1)(2n+1) |
| 6 |
| (6+n)(n-5) |
| 2 |
| 4 |
| 3 |
| 242 |
| 3 |
综上可知,Sn=
|
点评:本小题主要考查等差数列、等比数列、分组求和等知识,考查化归与转化的数学思想方法,以及运算求解能力和创新意识.

练习册系列答案
相关题目
已知O为坐标原点,P1、P2是双曲线
-
=1上的点.P是线段P1P2的中点,直线OP、P1P2的斜率分别为k1、k2,则k1k2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知椭圆C:
如图,已知椭圆C: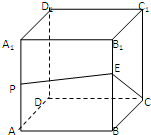 已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是
已知正方体ABCD-A1B1C1D1的棱长为2,P是AA1的中点,E是BB1上的点,则PE+EC的最小值是