题目内容
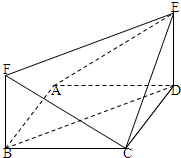 如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BF,DE⊥平面ABCD.
如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BF,DE⊥平面ABCD.(1)求证:CF∥平面ADE;
(2)求二面角C-EF-B的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用平面BCF中,有两条相交直线BC和BF平行于两一个平面中的两条相交直线 AD 和DE,得到平面
BCF∥平面ADE.
(2)连接AC,与BD交于M,取EF的中点N,连接MN,CN,则CM⊥平面EFBD,∠CNM是二面角C-EF-B的平面角,即可得出结论.
BCF∥平面ADE.
(2)连接AC,与BD交于M,取EF的中点N,连接MN,CN,则CM⊥平面EFBD,∠CNM是二面角C-EF-B的平面角,即可得出结论.
解答:
(1)证明:∵四边形ABCD为正方形,四边形BDEF为矩形,∴BC∥AD,BF∥DE,
这样,平面BCF中,有两条相交直线BC,BF平行于两一个平面中的两条相交直线AD,DE,
故有平面BCF∥平面ADE,
∴CF∥平面ADE.
(2)解:设BF=1,则AB=2,AC=2
,连接AC,与BD交于M,取EF的中点N,连接MN,CN,
则CM⊥平面EFBD,
∴∠CNM是二面角C-EF-B的平面角,
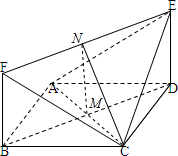
∵MN=1,CM=
,
∴CN=
,
∴cos∠CNM=
=
,
即二面角C-EF-B的余弦值为
.
这样,平面BCF中,有两条相交直线BC,BF平行于两一个平面中的两条相交直线AD,DE,
故有平面BCF∥平面ADE,
∴CF∥平面ADE.
(2)解:设BF=1,则AB=2,AC=2
| 2 |
则CM⊥平面EFBD,
∴∠CNM是二面角C-EF-B的平面角,

∵MN=1,CM=
| 2 |
∴CN=
| 3 |
∴cos∠CNM=
| MN |
| CN |
| ||
| 3 |
即二面角C-EF-B的余弦值为
| ||
| 3 |
点评:本题考查证明线面平行、面面平行的判定定理,考查二面角C-EF-B的余弦值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
不等式组
表示的平面区域是( )
|
A、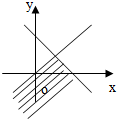 |
B、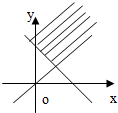 |
C、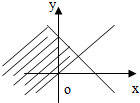 |
D、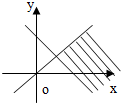 |
 如图,在边长为1的正方形OABC中任取一点P,分数以O、B为圆心,半径为
如图,在边长为1的正方形OABC中任取一点P,分数以O、B为圆心,半径为 如图,四棱柱的底面是菱形,各侧面都是长方形,两个对角面也是长方形,面积分别为Q1,Q.求四棱柱的侧面积.
如图,四棱柱的底面是菱形,各侧面都是长方形,两个对角面也是长方形,面积分别为Q1,Q.求四棱柱的侧面积.