题目内容
14.函数f(x)=x2-|x-$\frac{1}{4}$|的零点的个数为3.分析 方法1:由f(x)=0,得x2=|x-$\frac{1}{4}$|,转化为2个函数的交点个数问题进行求解即可.
方法2:直接由定义解方程f(x)=0即可.
解答 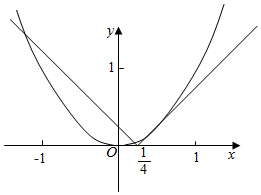 解:方法1:∵函数$f(x)={x^2}-|{x-\frac{1}{4}}|$,
解:方法1:∵函数$f(x)={x^2}-|{x-\frac{1}{4}}|$,
∴由f(x)=0,得x2=|x-$\frac{1}{4}$|,
作出函数y=x2和y=|x-$\frac{1}{4}$|的图象如图
则两个函数有3个交点,即函数的零点个数为3个.
法2:当x≥$\frac{1}{4}$时,f(x)=x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2,
由f(x)=x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2=0得x=$\frac{1}{2}$,
当x<$\frac{1}{4}$时,f(x)=x2+x-$\frac{1}{4}$=(x+$\frac{1}{2}$)2-$\frac{1}{2}$
由f(x)=(x+$\frac{1}{2}$)2-$\frac{1}{2}$=0得x+$\frac{1}{2}$=±$\sqrt{\frac{1}{2}}$=$±\frac{\sqrt{2}}{2}$,
则x=-$\frac{1}{2}$$±\frac{\sqrt{2}}{2}$,
即函数有3个零点,
故答案为:3.
点评 本题主要考查函数零点个数的判断,利用数形结合或定义法是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
2.关于命题p:A∩∅=∅,命题q:A∪∅=A,则下列说法正确的是( )
| A. | (¬p)∨q为假 | B. | (¬p)∧(¬q)为真 | C. | (¬p)∨(¬q)为假 | D. | (¬p)∧q为真 |
9.将函数y=f(x)的图象沿x轴向左平移π个单位后,再将所得图象上各点的横坐标缩小为原来的一半,得到函数y=sinx的图象,那么y=f(x)的表达式为( )
| A. | y=sin2x | B. | y=-sin2x | C. | $y=-cos\frac{x}{2}$ | D. | $y=-sin\frac{x}{2}$ |
19.已知α∈(0,π)且$cos({\frac{π}{4}+α})=\frac{3}{5}$,则cosα的值为( )
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
4.下列式子中表示正确的是( )
| A. | 2+cosx=4 | B. | $\sqrt{10}$>π | C. | sinx•cosx=sin2x | D. | sin75°>cos14° |
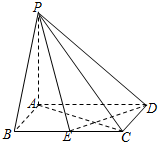 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.