题目内容
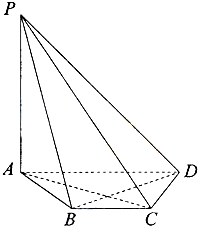
如图，在四棱锥P-ABCD中，PA⊥面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD．（1）证明：BD⊥PC；
（2）若PA=AD=4，BC=2，求四棱锥P-ABCD的体积．
考点：棱柱、棱锥、棱台的体积
专题：综合题,空间位置关系与距离
分析：（1）由PA⊥平面ABCD，AC⊥BD可证得BD⊥平面PAC，从而证得BD⊥PC；
（2）根据BC=2，AD=4，且ABCD是等腰梯形，且AC⊥BD，求SABCD，即可求VP-ABCD．
（2）根据BC=2，AD=4，且ABCD是等腰梯形，且AC⊥BD，求SABCD，即可求VP-ABCD．
解答：
（1）证明：∵PA⊥平面ABCD，BD?平面ABCD，
∴PA⊥BD，
又AC⊥BD，PA，AC是平面PAC内的两条相交直线，
∴BD⊥平面PAC，而PC?平面PAC，∴BD⊥PC…（5分）
（2）解：∵BC=2，AD=4，且ABCD是等腰梯形，且AC⊥BD
故S梯形ABCD=9…（8分）
又PA=4，故VP-ABCD=12…（12分）
（1）证明：∵PA⊥平面ABCD，BD?平面ABCD，∴PA⊥BD，
又AC⊥BD，PA，AC是平面PAC内的两条相交直线，
∴BD⊥平面PAC，而PC?平面PAC，∴BD⊥PC…（5分）
（2）解：∵BC=2，AD=4，且ABCD是等腰梯形，且AC⊥BD
故S梯形ABCD=9…（8分）
又PA=4，故VP-ABCD=12…（12分）
点评：本题考查直线与平面垂直判定定理与性质性质定理，考查直线与平面所成的角的应用与锥体体积，突出对分析、推理与计算能力的考查与应用，属于中档题．
练习册系列答案
相关题目
已知命题p：x=1是方程x+1=0的根；q：对于任意x∈R，总有|x|≥0，则下列命题为真命题的是（ ）
| A、p∧q | B、￢p∧￢q |
| C、p∧￢q | D、￢p∧q |
下列函数是奇函数的是（ ）
| A、y=x | ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x2，x∈[0，1] |
下列各项中表示的是同一函数的是（ ）
| A、y=2log2x与y=log2x2 |
| B、y=x与y=xlogxx |
| C、y=x与y=lnex |
| D、y=10lg|x|与y=lg10x |
已知函数y=2|x|，x∈R
如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC的中点．
已知函数f（x）=2x+1，g（x）=x2-2x+1．