题目内容
17.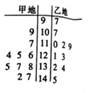 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.(1)分别计算甲、乙两地这10名学生的平均成绩;
(2)以样本估计总体,不通过计算,估计甲、乙两地学生成绩的偏差程度;
(3)在甲地被抽取的10位同学中,从成绩120分以上的8位同学中随机抽取2人,求恰有1名学生成绩在140分以上的概率.
分析 (1)利用茎叶图能分别计算甲、乙两地这10名学生的平均成绩.
(2)以样本估计总体,利用茎叶图能估计甲、乙两地学生成绩的偏差程度.
(3)在甲地被抽取的10位同学中,成绩120分以上的有8人,其中2人的成绩在140人以上,由此利用等可能事件概率计算公式能求出恰有1名学生成绩在140分以上的概率.
解答 解:(1)甲地这10名学生的平均成绩$\overline{{x}_{甲}}$=$\frac{1}{10}$(109+117+124+125+126+135+137+138+142+147)=130,
乙地这10名学生的平均成绩$\overline{{x}_{乙}}$=$\frac{1}{10}$(97+107+110+112+119+121+123+132+134+145)=120.
(2)由茎叶图得到甲的成绩相对集中,乙的成绩相对分散,
∴甲地学生成绩的偏差程度小、乙地学生成绩的偏差程度大.
(3)在甲地被抽取的10位同学中,成绩120分以上的有8人,其中2人的成绩在140人以上,
∴从成绩120分以上的8位同学中随机抽取2人,基本事件总数n=${C}_{8}^{2}=28$,
恰有1名学生成绩在140分以上包含的基本事件个数m=${C}_{8}^{1}{C}_{2}^{1}=16$,
∴恰有1名学生成绩在140分以上的概率p=$\frac{m}{n}=\frac{16}{28}$=$\frac{4}{7}$.
点评 本题考查茎叶图、古典概型、概率等基础知识,考查数据处理能力、运算求解能力,考查函数与方程思想、集合思想,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
12.数列{an}首项a1=1,对于任意m,n∈N*,有an+m=an+3m,则{an}前5项和S5=( )
| A. | 121 | B. | 25 | C. | 31 | D. | 35 |
2.《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代具有很高的数学水平,其求法是“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂,减上,余四约之,为实,一为从偶,开平方得积”,若把这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,现有周长为10的△ABC满足sinA:sinB:sin:C=5:7:8,试用以上给出的公式求得△ABC的面积为( )
| A. | $\frac{5}{8}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 10$\sqrt{3}$ | D. | $\frac{35}{8}$ |
9.y=$tan(4x+\frac{π}{3})$的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
5.已知向量$\overrightarrow a$表示“向东航行3km”,向量$\overrightarrow b$表示“向南航行3km,则$\overrightarrow a$+$\overrightarrow b$表示( )
| A. | 向东南航行6km | B. | 向东南航行3$\sqrt{2}$km | C. | 向东北航行3$\sqrt{2}$km | D. | 向东北航行6km |
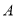 如果满足:①
如果满足:① ;②若对
;②若对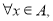 有
有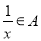 ,则称
,则称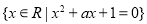 ;
;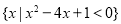 ;
; .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )