题目内容
12.数列{an}首项a1=1,对于任意m,n∈N*,有an+m=an+3m,则{an}前5项和S5=( )| A. | 121 | B. | 25 | C. | 31 | D. | 35 |
分析 推导出{an}是首项为1,公差为3的等差数列,由此能求出{an}前5项和S5.
解答 解:∵数列{an}首项a1=1,对于任意m,n∈N*,有an+m=an+3m,
∴an+1=an+3,
∴{an}是首项为1,公差为3的等差数列,
∴{an}前5项和S5=5a1+$\frac{5×4}{2}×d$=$5×1+\frac{5×4}{2}×3$=35.
故选:D.
点评 本题考查等差数列的前5项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.某商场对A商品近30天的日销售量y(件)与时间t(天)的销售情况进行整理,得到如下数据统计分析,日销售量y(件)与时间t(天)之间具有线性相关关系
(1)请根据表提供的数据,用最小二乘法原理求出y关于t的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+a
(2)已知A商品近30天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{-t+100,(20≤t≤30,t∈N)}\\{t+20,(0<t<20,t∈Z)}\end{array}\right.$
根据(1)中求出的线性回归方程,预测t为何值时,A商品的日销售额最大(参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}\overline{t}$)
| 时间(t) | 2 | 4 | 6 | 8 | 10 |
| 日销售量(y) | 38 | 37 | 32 | 33 | 30 |
(2)已知A商品近30天内的销售价格Z(元)与时间t(天)的关系为:z=$\left\{\begin{array}{l}{-t+100,(20≤t≤30,t∈N)}\\{t+20,(0<t<20,t∈Z)}\end{array}\right.$
根据(1)中求出的线性回归方程,预测t为何值时,A商品的日销售额最大(参考公式$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}\overline{t}$)
 ,若
,若 ,则实数
,则实数 的值是 .
的值是 .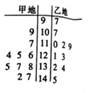 已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示.
已知在一次期末数学测试中,教育局在某市甲、乙两地各抽取了10名学生的成绩做调查,所的情况如下所示. 中,
中, ,
, ,
, ,则( )
,则( ) 或
或 B.
B.
 D.以上答案都不对
D.以上答案都不对