题目内容
5.点(1,-2,3)关于x轴的对称点坐标为( )| A. | (1,2,-3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (-1,2,3) |
分析 关于x轴的对称点坐标的性质:横坐标不变,纵坐标变为相反数,竖坐标变为相反数.
解答 解:点(1,-2,3)关于x轴的对称点坐标为(1,2,-3).
故选:A.
点评 本题考查空间中点的坐标的求法,是基础题,解题时要认真审题,注意对称的性质的合理运用.

练习册系列答案
相关题目
16.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=x3 | B. | y=ln|x| | C. | y=-x2 | D. | y=2x |
13.函数y=$\sqrt{9-{x}^{2}}$,x∈[-3,3]的值域为( )
| A. | (-∞,3] | B. | [3,+∞) | C. | [0,3] | D. | (0,3] |
10.已知tanx=2,则$\frac{2cosx-sinx}{cosx}$( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
17.已知a,b∈R,函数f(x)=ax-b,若对任意x∈[-1,1],有0≤f(x)≤1,则$\frac{3a+b+1}{a+2b-2}$的取值范围为( )
| A. | [-$\frac{1}{2}$,0] | B. | [-$\frac{4}{5}$,0] | C. | [-$\frac{1}{2}$,$\frac{2}{7}$] | D. | [-$\frac{4}{5}$,$\frac{2}{7}$] |
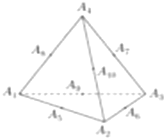 已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.
已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.