题目内容
4.函数f(x)的定义域为R,且f(-3)=1,f'(x)>2,则不等式f(x)<2x+7的解集为(-∞,-3).分析 设F(x)=f(x)-(2x+7),则F′(x)=f′(x)-2,由对任意x∈R总有f′(x)>2,知F′(x)=f′(x)-2>0,所以F(x)=f(x)-2x-7在R上是增函数,由此能够求出结果.
解答 解:设F(x)=f(x)-(2x+7)=f(x)-2x-7,
则F′(x)=f′(x)-2,
∵f′(x)>2,
∴F′(x)=f′(x)-2>0,
∴F(x)=f(x)-2x-7在R上递增,
∵f(-3)=1,
∴F(-3)=f(-3)-2×(-3)-7=0,
∵f(x)<2x+7,
∴F(x)=f(x)-2x-7<0,
∴x<-3,
故答案为:(-∞,-3).
点评 本题考查利用导数研究函数的单调性的应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
14.已知正数a,b,c满足2a-b+c=0,则$\frac{ac}{{b}^{2}}$的最大值为( )
| A. | 8 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
13.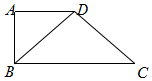 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
| A. | 面ABD⊥面ABC | B. | 面ADC⊥面BDC | C. | 面ABC⊥面BDC | D. | 面ADC⊥面ABC |
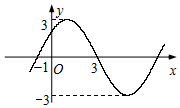 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$. 如图,四边形ABCD是一个5×4的方格纸,向此四边形内抛撒一粒小豆子,则小豆子恰好落在阴影部分内的概率为$\frac{1}{5}$.
如图,四边形ABCD是一个5×4的方格纸,向此四边形内抛撒一粒小豆子,则小豆子恰好落在阴影部分内的概率为$\frac{1}{5}$.