题目内容
6.已知函数$f(x)=\left\{\begin{array}{l}x,|x|≤1\\ sin\frac{π}{2}x,|x|>1\end{array}\right.$则下列结论正确的是( )| A. | 函数f(x)在$[-\frac{π}{2},\frac{π}{2}]$上单调递增 | B. | 函数f(x)的值域是[-1,1] | ||
| C. | ?x0∈R,f(-x0)≠-f(x0) | D. | ?x∈R,f(-x)≠f(x) |
分析 根据分段函数的表达式,作出函数f(x)的图象,根据函数单调性,值域以及奇偶性的性质进行判断即可.
解答 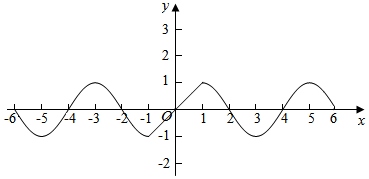 解:作出f(x)的图象如图,
解:作出f(x)的图象如图,
A.则函数在[-1,1]上为增函数,则[1,$\frac{π}{2}$]上是减函数,则函数f(x)在$[-\frac{π}{2},\frac{π}{2}]$上单调递增错误,
B.函数f(x)的值域是[-1,1],故B正确,
C.当-1≤x≤1时,满足f(-x)=-f(x),故C错误,
D.当x=2时,f(-2)=f(2)=0,此时?x∈R,f(-x)≠f(x)不成立,故D错误,
故选:B.
点评 本题主要考查命题的真假判断,利用分段函数的表达式,作出函数的图象,利用函数的性质是解决本题的关键.

练习册系列答案
相关题目
16.在△ABC中,角A,B,C所对的边是a,b,c,已知a=2,则bcosC+ccosB等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 4 | D. | 2 |
11.已知F1、F2是椭圆的两个焦点,若存在满足$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0的点M在椭圆外部,则椭圆离心率的取值范围是( )
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,1) |
18.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-3x(x≥0)}\\{ln(1-x)(x<0)}\end{array}\right.$,若|f(x)+4|≥a(x-1),则a的取值范围是( )
| A. | [-1,3] | B. | [0,6] | C. | [0,5] | D. | [0,12] |