题目内容
11.已知F1、F2是椭圆的两个焦点,若存在满足$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0的点M在椭圆外部,则椭圆离心率的取值范围是( )| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | [$\frac{\sqrt{2}}{2}$,1) |
分析 由已知得顶角(F1、F2与短轴端点形成的角)为钝角,从而c>b,由此能求出椭圆离心率的取值范围.
解答 解:∵F1、F2是椭圆的两个焦点,存在满足$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0的点M在椭圆外部,
∴顶角(F1、F2与短轴端点形成的角)为钝角,
∴c>b,∴c2>b2=a2-c2,∴2c2>a2,
∴a<$\sqrt{2}c$,
∴e=$\frac{c}{a}$>$\frac{\sqrt{2}}{2}$,
又0<e<1,
∴椭圆离心率的取值范围是($\frac{\sqrt{2}}{2}$,1).
故选:C.
点评 本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}x,|x|≤1\\ sin\frac{π}{2}x,|x|>1\end{array}\right.$则下列结论正确的是( )
| A. | 函数f(x)在$[-\frac{π}{2},\frac{π}{2}]$上单调递增 | B. | 函数f(x)的值域是[-1,1] | ||
| C. | ?x0∈R,f(-x0)≠-f(x0) | D. | ?x∈R,f(-x)≠f(x) |
3.幂函数y=xa在x=1处切线方程为y=-4x,则a的值为( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
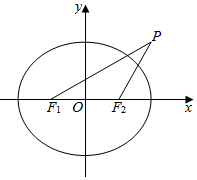 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.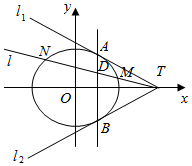 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的两条切线方程y=±$\frac{1}{2}$(x-4),切点分别为A、B,且切线与x轴的交点为T.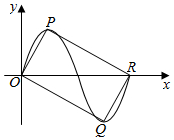 如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.
如图,四边形OQRP为矩形,其中P,Q分别是函数f(x)=$\sqrt{3}$sinwx(A>0,w>0)图象上的一个最高点和最低点,O为坐标原点,R为图象与x轴的交点.