题目内容
19.己知命题p:“a>b”是“2a>2b”的充要条件;q:?x∈R,ex<lnx,则( )| A. | ¬p∨q为真命题 | B. | p∧¬q为假命题 | C. | p∧q为真命题 | D. | p∨q为真命题 |
分析 命题p:“a>b”?“2a>2b”,即可判断出真假.q:令f(x)=ex-lnx,x∈(0,1]时,f(x)>0;x>1时,f′(x)=${e}^{x}-\frac{1}{x}$,因此x>1时,f(x)单调递增,可得f(x)>0.即可判断出真假.
解答 解:命题p:“a>b”?“2a>2b”,是真命题.
q:令f(x)=ex-lnx,f′(x)=${e}^{x}-\frac{1}{x}$.x∈(0,1]时,f(x)>0;x>1时,f(x)单调递增,∴f(x)>f(1)=e>0.
∴不存在x∈R,ex<lnx,是假命题.
∴只有p∨q为真命题.
故选:D.
点评 本题考查了复合命题真假的判定方法、指数函数的单调性、利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知$\overrightarrow a=({4,2})$,则与$\overrightarrow a$方向相反的单位向量的坐标为( )
| A. | (2,1) | B. | (-2,-1) | C. | $({\frac{{2\sqrt{5}}}{5},\frac{{\sqrt{5}}}{5}})$ | D. | $({-\frac{{2\sqrt{5}}}{5},-\frac{{\sqrt{5}}}{5}})$ |
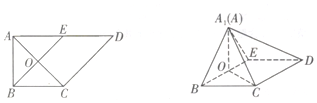 如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙
如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙