题目内容
1.ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=$\frac{a}{3}$,过PMN的平面交上底面于PQ,Q在CD上,则PQ等于( )| A. | $\frac{\sqrt{2}}{2}$a | B. | $\frac{\sqrt{2}}{4}$a | C. | $\frac{\sqrt{2}}{3}$a | D. | $\frac{2\sqrt{2}}{3}$a |
分析 由已知得MN∥PQ.DP=DQ=$\frac{2a}{3}$,由此利用勾股定理能求出PQ.
解答 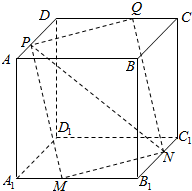 解:∵ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,
解:∵ABCD-A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,
P是上底面的棱AD上的一点,AP=$\frac{a}{3}$,过PMN的平面交上底面于PQ,Q在CD上,
∴平面ABCD∥平面A1B1C1D1,
∴MN∥PQ.
∵M,N分别是A1B1,B1C1的中点,AP=$\frac{a}{3}$,
∴CQ=$\frac{a}{3}$,∴DP=DQ=$\frac{2a}{3}$,
∴PQ=$\sqrt{D{P}^{2}+D{Q}^{2}}$=$\sqrt{\frac{4{a}^{2}}{9}+\frac{4{a}^{2}}{9}}$=$\frac{2\sqrt{2}}{3}a$.
故选:D.
点评 本题考查线段和的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
11.下列函数为偶函数的是( )
| A. | f(x)=x | B. | f(x)=x2 | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2-2x+1 |
6.已知集合M={x|x2+5x-6≤0},N={x|x2-16<0},则M∩N=( )
| A. | (-4,1] | B. | [1,4] | C. | [-6,-4) | D. | [-6,4) |
11.若幂函数$f(x)={x^{{a^2}-2a-3}}$在(0+∞)上为减函数,则实数a的取值范围是( )
| A. | (-∞,-1)∪(3,+∞) | B. | (-1,3) | C. | (-∞,-1]∪[3,+∞) | D. | [-1,3] |