题目内容
16.直线2ax+(a2+1)y-1=0的倾斜角的取值范围是( )| A. | [$\frac{π}{4}$,$\frac{3π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | C. | (0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) |
分析 设直线2ax+(a2+1)y-1=0的倾斜角为θ,可得tanθ=-$\frac{2a}{{a}^{2}+1}$,对a分类讨论,利用基本不等式的性质、三角函数求值即可得出.
解答 解:设直线2ax+(a2+1)y-1=0的倾斜角为θ,
则tanθ=-$\frac{2a}{{a}^{2}+1}$,
a=0时,tanθ=0,可得θ=0;
a>0时,tanθ≥$-\frac{2a}{2a}$=-1,当且仅当a=1时取等号,∴θ∈$[\frac{3π}{4},π)$;
a<0时,tanθ≤1,当且仅当a=-1时取等号,∴θ∈$(0,\frac{π}{4}]$;
综上可得:θ∈$[0,\frac{π}{4}]$∪$[\frac{3π}{4},π)$.
故选:D.
点评 本题考查了基本不等式的性质、三角函数求值、分类讨论方法、倾斜角与斜率的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.下列不等式成立的是( )
| A. | 若a>b>0,则$\frac{b}{a}$>$\frac{b+1}{a+1}$ | B. | 若a>b>0,则lg$\frac{a+b}{2}$<$\frac{lga+lgb}{2}$ | ||
| C. | 若a>b>0,则a+$\frac{1}{b}$>b+$\frac{1}{a}$ | D. | 若a>b>0,则$\sqrt{a}-\sqrt{b}$>$\sqrt{a-b}$ |
1.直线m:x+(a2-1)y+1=0,直线n:x+(2-2a)y-1=0,则“a=-3”是“直线m、n关于原点对称”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.执行如图所示的程序框图,输出k的值为( )
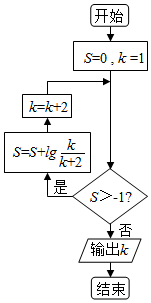

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
5.复数z满足z(1-i)=|1+i|,则复数z的共轭复数在复平面内的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 在正三棱柱ABC-A1B1C1中,AB=$\sqrt{2}$AA1,求证:BC1=AB1.
在正三棱柱ABC-A1B1C1中,AB=$\sqrt{2}$AA1,求证:BC1=AB1.