题目内容
6.下列不等式成立的是( )| A. | 若a>b>0,则$\frac{b}{a}$>$\frac{b+1}{a+1}$ | B. | 若a>b>0,则lg$\frac{a+b}{2}$<$\frac{lga+lgb}{2}$ | ||
| C. | 若a>b>0,则a+$\frac{1}{b}$>b+$\frac{1}{a}$ | D. | 若a>b>0,则$\sqrt{a}-\sqrt{b}$>$\sqrt{a-b}$ |
分析 A.作差即可判断出结论;
B.利用对数的运算性质、基本不等式的性质即可判断出结论;
C.作差即可判断出结论;
D.取a=2,b=1,可得$\sqrt{a}-\sqrt{b}$=$\sqrt{2}$-1<$\sqrt{2-1}$=$\sqrt{a-b}$,即可判断出结论.
解答 解:A.a>b>0,则$\frac{b}{a}$-$\frac{b+1}{a+1}$=$\frac{b-a}{a(a+1)}$<0,∴$\frac{b}{a}$<$\frac{b+1}{a+1}$,因此A不成立;
B.a>b>0,则lg$\frac{a+b}{2}$>$lg\sqrt{ab}$=$\frac{lga+lgb}{2}$,因此B不成立;
C.a>b>0,则a+$\frac{1}{b}$-(b+$\frac{1}{a}$)=(a-b)$(1+\frac{1}{ab})$>0,因此正确;
D.a>b>0,则取a=2,b=1,则$\sqrt{a}-\sqrt{b}$=$\sqrt{2}$-1<$\sqrt{2-1}$=$\sqrt{a-b}$,因此不成立.
故选:C.
点评 本题考查了基本不等式的性质、作差法比较两个数的大小方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.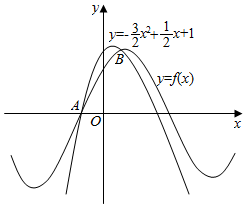 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )| A. | f(x)=sin($\frac{1}{6}$x+$\frac{π}{3}$) | B. | f(x)=sin($\frac{1}{2}$x+$\frac{π}{3}$) | C. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$) | D. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{6}$) |
11.命题“若a2<b,则-$\sqrt{b}$<a<$\sqrt{b}$”的逆否命题为( )
| A. | 若a2≥b,则a≥$\sqrt{b}$或a≤-$\sqrt{b}$ | B. | 若a2≥b,则a>$\sqrt{b}$或a<-$\sqrt{b}$ | ||
| C. | 若a≥$\sqrt{b}$或a≤-$\sqrt{b}$,则a2≥b | D. | 若a>$\sqrt{b}$或a<-$\sqrt{b}$,则a2≥b |
15.设集合M={x|x2-x-6<0},N={x|x-1>0},则M∩N=( )
| A. | (1,2) | B. | (1,3) | C. | (-1,2) | D. | (-1,3) |
16.直线2ax+(a2+1)y-1=0的倾斜角的取值范围是( )
| A. | [$\frac{π}{4}$,$\frac{3π}{4}$] | B. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | C. | (0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π) |
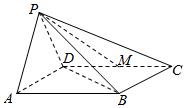 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,PA=PD,M为CD的中点,BD⊥PM.