题目内容
某学校推荐甲、乙、丙、丁4名同学参加A、B、C三所大学的自主招生考试.每名同学只推荐一所大学,每所大学至少推荐一名.则不推荐甲同学到A大学的推荐方案有( )
| A、24种 | B、48种 |
| C、54种 | D、60种 |
考点:计数原理的应用
专题:排列组合
分析:分类讨论:甲在B、C两所大学选一所,其余3位同学,未选甲选的学校;有一位选甲选的学校,相加后得到结果.
解答:
解:分类讨论:甲在B、C两所大学选一所,其余3位同学,未选甲选的学校,共有
•
=12种;
甲在B、C两所大学选一所,其余3位同学,有一位选甲选的学校,共有
=12种,
故共有12+12=24种,
故选:A.
| C | 1 2 |
| •C | 2 3 |
| A | 2 2 |
甲在B、C两所大学选一所,其余3位同学,有一位选甲选的学校,共有
| C | 1 2 |
| •C | 1 3 |
| •A | 2 2 |
故共有12+12=24种,
故选:A.
点评:本题考查排列组合的实际应用,本题解题的关键是其余3位同学,要分类讨论.

练习册系列答案
相关题目
执行如图所示的程序框图,则输出的T值为( )


| A、55 | B、30 | C、91 | D、100 |
执行如图所示的程序框图,输出的c值为( )


| A、5 | B、8 | C、13 | D、21 |
(3x-1)5的展开式中x2项的系数为( )
| A、90 | B、270 |
| C、-90 | D、-270 |
定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f(
)=
f(x),且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
)的值为( )
| x |
| 3 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
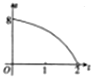
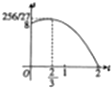
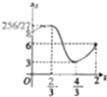
 如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )
如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )