题目内容
7.已知一个长方体的表面积为48(单位:cm2),12条棱长度之和为36(单位:cm),则这个长方体的体积的取值范围是[16,20](单位:cm3).分析 求出体积关于c的函数,利用导数确定函数的单调性,即可得出结论.
解答 解:设长方体的三条棱长分别为a,b,c,则a+b+c=9,ab+bc+ac=24,
化简可得V=abc=c(c2-9c+24),c的范围[1,5]
∴V′=3(c-2)(c-4),
∴函数在(1,2),(4,5)上单调递增,(2,4)上单调递减,
c=2时,V=20,c=4时,V=16,
∴这个长方体的体积的取值范围是[16,20].
故答案为:[16,20].
点评 本题考查长方体体积的计算,考查导数知识的运用,属于中档题.

练习册系列答案
相关题目
18.二次不等式-$\frac{a}{3}$x2+2bx-c<0的解集是全体实数的充要条件是( )
| A. | $\left\{\begin{array}{l}{a>0}\\{4{b}^{2}-\frac{4}{3}ac<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a>0}\\{4{b}^{2}-\frac{4}{3}ac>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a<0}\\{4{b}^{2}-\frac{4}{3}ac>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a<0}\\{4{b}^{2}-\frac{4}{3}ac<0}\end{array}\right.$ |
15.过双曲线的一个焦点F2作垂直干实轴的弦PQ,F1是另一焦点,若∠PF1Q=$\frac{π}{2}$,则双曲线的离心率e等于( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$+1 |
2.函数f(x)在定义域(0,+∞)内恒满足:①f(x)>0;②2f(x)<xf′(x)<3f(x),其中f′(x)为f(x)的导函数,则( )
| A. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ | B. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | C. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ | D. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ |
17.在空间四面体EFGH中,点I是面FGH的重心,则$\overrightarrow{EI}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{EF}$+$\frac{1}{2}$$\overrightarrow{EG}$+$\frac{1}{2}$$\overrightarrow{EH}$ | B. | $\frac{1}{5}$$\overrightarrow{EF}$+$\frac{1}{5}$$\overrightarrow{EG}$+$\frac{1}{5}$$\overrightarrow{EH}$ | C. | $\frac{1}{4}$$\overrightarrow{EF}$+$\frac{1}{4}$$\overrightarrow{EG}$+$\frac{1}{4}$$\overrightarrow{EH}$ | D. | $\frac{1}{3}$$\overrightarrow{EF}$+$\frac{1}{3}$$\overrightarrow{EG}$+$\frac{1}{3}$$\overrightarrow{EH}$ |
 如图,茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员的平均成绩相同,则成绩较为稳定的运动员成绩的方差为2.
如图,茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员的平均成绩相同,则成绩较为稳定的运动员成绩的方差为2.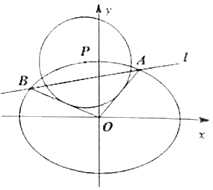 如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.
如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.