Question

16．设函数f（x）=x•e^cosx（x∈[-π，π]）的图象大致是（　　）

• A．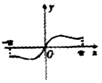
• B．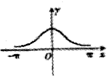
• C．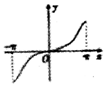
• D．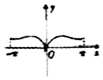

Answer 1

分析 判断函数的奇偶性，排除选项，利用函数的导数判断函数的单调性，判断函数的图象即可．

解答 解：函数f（x）=x•e^cosx（x∈[-π，π]）是奇函数，排除B，C，
当x＞0时，函数f′（x）=e^cosx（1-xsinx），令e^cosx（1-xsinx）=0，可得xsinx=1，
当x=$\frac{π}{4}$时，$\frac{π}{4}$sin$\frac{π}{4}$=$\frac{\sqrt{2}π}{8}$＜1，x=$\frac{π}{2}$时，$\frac{π}{2}sin\frac{π}{2}$＞1，
xsinx=1的一个零点x₁，在（$\frac{π}{4}$，$\frac{π}{2}$）之间，x∈（0，x₁）时，f′（x）＞0，函数是增函数，
当x=$\frac{3π}{4}$时，$\frac{3π}{4}$sin$\frac{3π}{4}$=$\frac{3\sqrt{2}π}{8}$＞1，x=π时，πsinπ=0＜1，
xsinx=1的令一个零点x₂，在（$\frac{3π}{4}$，π）之间，
x∈（x₁，x₂），f′（x）＜0，函数是减函数，
x∈（x₂，π），f′（x）＞0，函数是增函数，
所以排除C．
故选：A．

点评 本题考查函数的图象的判断与应用，函数的导数的应用，注意函数的奇偶性以及单调性的判断．