题目内容
1.某几何体的一条棱长为3,在该几何体的正视图中,这条棱的投影长为2的线段,在该几何体的侧视图和俯视图中,这条棱长的投影长分别是a和b的线段,则a+b的最大值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{7}$ | C. | 4 | D. | 2$\sqrt{6}$ |
分析 由棱和它在三视图中的投影扩展为长方体,三视图中的三个投影,是三个面对角线,设出三度,利用勾股定理,基本不等式求出最大值.
解答 解:将已知中的棱和它在三视图中的投影扩展为长方体,
三视图中的三个投影,是三个面对角线,
则设长方体的三度:x、y、z,
所以x2+y2+z2=9,x2+y2=a2,y2+z2=b2,
x2+z2=4可得a2+b2=14
∵(a+b)2≤2(a2+b2)
a+b≤2$\sqrt{7}$,
∴a+b的最大值为2$\sqrt{7}$,
故选:B.
点评 本题考查三视图,几何体的结构特征,考查空间想象能力,基本不等式的应用,是中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
6.已知函数f(x)=kx-2,f(1)=-1,则f(2)=( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
7.已知sinα<0且tanα>0,则角α所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知函数f(x)=-x2-2x,g(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{x+\frac{1}{4x},x>0}\end{array}\right.$,若函数y=g(f(x))-a有4个零点,则实数a的取值范围是( )
| A. | (0,1] | B. | ($\frac{1}{2}$,1] | C. | ($\frac{1}{2}$,$\frac{5}{4}$) | D. | [1,$\frac{5}{4}$) |
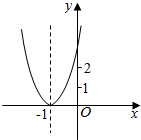 已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论:①abc<0;②b2-4ac=0;③a>2;④4a-2b+c>0.其中正确结论的个数是( )