题目内容
3.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x,若函数f(x)的定义域与值域都是[1,a],则对于任意的x1,x2∈[1,a+1]时,总有$|{f({x_1})-g({x_2})}|≤{t^2}+2t-1$恒成立,则t的取值范围为( )| A. | [1,3] | B. | [-1,3] | C. | [1,+∞)∪(-∞,-3] | D. | [3,+∞)∪(-∞,-1] |
分析 根据二次函数的对称轴判断出函数单调性,得出a=f(1),求出a=2,进而求出只需t2+2t-3≥0,得出答案.
解答 解:函数f(x)=x2-2ax+5(a>1)的对称轴为x=a∈[1,a]
∴函数f(x)=x2-2ax+5(a>1)在[1,a]上单调递减
∵函数f(x)的定义域和值域均为[1,a]
∴a=f(1)
∴a=2
∴f(x)=x2-4x+5,g(x)=log3x.
∵对于任意的x1,x2∈[1,3],1≤f(x)≤2,0≤g(x)≤1,
∴t2+2t-3≥0,
∴t∈[1,+∞)∪(-∞,-3].
故选:C.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
18.某三棱锥的三视图如图所示,其中左视图中虚线平分底边,则该三棱锥的所有面中最大面的面积是( )
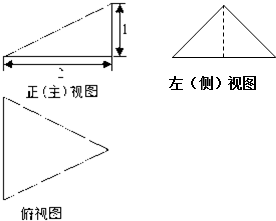

| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
8.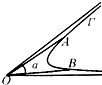 如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
 如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )
如图,曲线Γ在顶点为O的角α的内部,A、B是曲线Γ上任意相异两点,且α≥∠AOB,我们把满足条件的最小角叫做曲线Γ相对于点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{4+\frac{{x}^{2}}{3}}(x≤0)}\\{2{x}^{2}-3x+2(x>0)}\end{array}\right.$,那么它相对于点O的“确界角”等于( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
12.已知抛物线y2=4x的准线与双曲线4x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)交于A、B两点,点F为抛物线的焦点,若△FAB为直角三角形,则双曲线离心率为( )
| A. | $\frac{\sqrt{17}}{2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\frac{\sqrt{57}}{3}$ | D. | $\frac{8}{3}$ |
13.执行如图的程序框图,如果输入的n是3,那么输出的p是( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{24}$ | D. | $\frac{1}{120}$ |
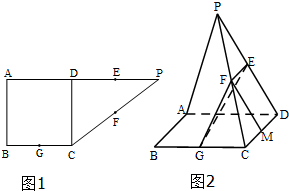 如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.
如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点. 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-1,0),F2(1,0),上、下顶点分别为B1、B2,右准线l:x=4. 如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.
如图,在圆C:(x+1)2+y2=16内有一点A(1,0),Q为圆C上一点,AQ的垂直平分线与C、Q的连线交于点M.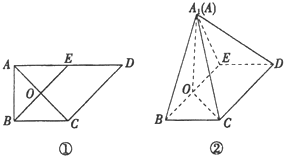 如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.
如图①,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=$\sqrt{2}$,AD=2$\sqrt{2}$,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图②.