题目内容
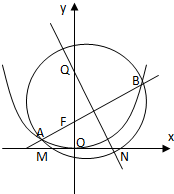 已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5).
已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5).(1)求p的值;
(2)以AB为直径的圆交x轴于点M,N,记劣弧
 |
| MN |
| S |
| |AB| |
考点:直线与圆锥曲线的综合问题,直线与圆的位置关系
专题:圆锥曲线的定义、性质与方程
分析:(1)求出l的方程为y=x+
,设A(x1,y1),B(x2,y2),联立直线与抛物线方程,利用韦达定理求出AB中点坐标,推出中垂线方程,结合AB的中垂线交y轴于点Q(0,5).求出p即可.
(2)设l的方程为y=kx+1,代入x2=4y,求出AB的距离以及AB中点为D(2k,2k2+1),令∠MDN=2α,求出S的表达式,推出关系式
=α,利用D到x轴的距离|DE|=2k2+1,求出cosα=
=
,然后求解
的最大值.
| p |
| 2 |
(2)设l的方程为y=kx+1,代入x2=4y,求出AB的距离以及AB中点为D(2k,2k2+1),令∠MDN=2α,求出S的表达式,推出关系式
| S |
| |AB| |
| |DE| | ||
|
| 2k2+1 |
| 2k2+2 |
| S |
| |AB| |
解答:
解:(1)抛物线C:x2=2py(p>0)的焦点为F,F(0,
),
当l的倾斜角为45°时,l的方程为y=x+
设A(x1,y1),B(x2,y2),
由
,得x2-2px-p2=0,
x1+x2=2p,y1+y2=x1+x2+p=3p,得AB中点为D(p,
p)…(3分)
AB中垂线为y-
p=-(x-p),
x=0代入得y=
p=5.
∴p=2…(6分)
(2)设l的方程为y=kx+1,代入x2=4y得x2-4kx-4=0,
|AB|=y1+y2+2=k(x1+x2)+4=4k2+4,
AB中点为D(2k,2k2+1)
令∠MDN=2α,S=2α•
|AB|=α•|AB|,
∴
=α…(8分)
D到x轴的距离|DE|=2k2+1,
cosα=
=
…(10分)
当k2=0时cosα取最小值
,α的最大值为
.
故
的最大值为
.…(12分)
| p |
| 2 |
当l的倾斜角为45°时,l的方程为y=x+
| p |
| 2 |
设A(x1,y1),B(x2,y2),
由
|
x1+x2=2p,y1+y2=x1+x2+p=3p,得AB中点为D(p,
| 3 |
| 2 |
AB中垂线为y-
| 3 |
| 2 |
x=0代入得y=
| 5 |
| 2 |
∴p=2…(6分)
(2)设l的方程为y=kx+1,代入x2=4y得x2-4kx-4=0,
|AB|=y1+y2+2=k(x1+x2)+4=4k2+4,
AB中点为D(2k,2k2+1)
令∠MDN=2α,S=2α•
| 1 |
| 2 |
∴
| S |
| |AB| |
D到x轴的距离|DE|=2k2+1,
cosα=
| |DE| | ||
|
| 2k2+1 |
| 2k2+2 |
当k2=0时cosα取最小值
| 1 |
| 2 |
| π |
| 3 |
故
| S |
| |AB| |
| π |
| 3 |
点评:本题考查直线与抛物线方程的位置关系,直线与直线的位置关系,以及圆的方程的综合应用,考查分析问题解决问题的能力,转化思想的应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
从4男3女志愿者中,选1女2男分别到A,B,C地执行任务,则不同的选派方法( )
| A、36种 | B、108种 |
| C、210种 | D、72种 |
执行如图所示程序框图的算法,输出的结果为( )


| A、log910 |
| B、lg11 |
| C、2 |
| D、log310 |
若幂函数f(x)=mxα的图象经过点A(
,
),则它在点A处的切线方程是( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、2x-y=0 |
| B、2x+y=0 |
| C、4x-4y+1=0 |
| D、4x+4y+1=0 |